题目内容
【题目】如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心. 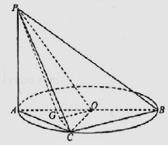
(1)求证:平面OPG⊥平面PAC;
(2)若PA=AB=2AC=2,求二面角A﹣OP﹣G的余弦值.
【答案】
(1)证明:如图,延长OG交AC于点M.

因为G为△AOC的重心,所以M为AC的中点.
因为O为AB的中点,所以OM∥BC.
因为AB是圆O的直径,所以BC⊥AC,所以OM⊥AC.
因为PA⊥平面ABC,OM平面ABC,所以PA⊥OM.
又PA平面PAC,AC平面PAC,PA∩AC=A,所以OM⊥平面PAC.
即OG⊥平面PAC,又OG平面OPG,
所以平面OPG⊥平面PAC
(2)解:以点C为原点, ![]() 方向分别为x,y,z轴正方向建立空间直角坐标系Cxyz,
方向分别为x,y,z轴正方向建立空间直角坐标系Cxyz,
则C(0,0,0), ![]() ,
,
则 ![]() .
.
平面OPG即为平面OPM,设平面OPM的一个法向量 ![]() ,
,
则 
令z=1,得 ![]() .
.
过点C作CH⊥AB于点H,由PA⊥平面ABC,
易得CH⊥PA,又PA∩AB=A,所以CH⊥平面PAB,即CH为平面PAO的一个法向量.
在Rt△ABC中,由AB=2AC,得∠ABC=30°,则 ![]() .
.
所以 ![]() ,
,
所以 ![]() .
.
设二面角A﹣OP﹣G的大小为θ,
则 
即二面角A﹣OP﹣G的余弦值为 ![]() .
.

【解析】(1)延长OG交AC于点M.可得OM∥BC.由AB是圆O的直径,得OM⊥AC.由PA⊥平面ABC,可得OM⊥平面PAC.即OG⊥平面PAC,证得平面OPG⊥平面PAC.(2)以点C为原点, ![]() 方向分别为x,y,z轴正方向建立空间直角坐标系Cxyz,则C(0,0,0),
方向分别为x,y,z轴正方向建立空间直角坐标系Cxyz,则C(0,0,0), ![]() 利用向量法求解.
利用向量法求解.
【考点精析】通过灵活运用平面与平面垂直的判定,掌握一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A﹣BCD的外接球,BC=3,AB=2 ![]() ,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
【题目】某校期中考试后,按照学生的数学考试成绩优秀和不优秀进行统计,得到如下列联表:
优秀 | 不优秀 | 总计 | |
文科 | 60 | 140 | 200 |
理科 | 265 | 335 | 600 |
总计 | 325 | 475 | 800 |
(1)画出列联表的等高条形图,并通过图形判断数学成绩与文理分科是否有关;
(2)利用独立性检验,分析文理分科对学生的数学成绩是否有影响.


