题目内容
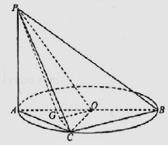
【题目】如图,在三棱台DEF﹣ABC中,AB=2DE,G,H分别为AC,BC的中点. 
(Ⅰ)求证:BD∥平面FGH;
(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.
【答案】解:(Ⅰ)证明:根据已知条件,DF∥AC,EF∥BC,DE∥AB; △DEF∽△ABC,又AB=2DE,
∴BC=2EF=2BH,
∴四边形EFHB为平行四边形;
∴BE∥HF,HF平面FGH,BE平面FGH;
∴BE∥平面FGH;
同样,因为GH为△ABC中位线,∴GH∥AB;
又DE∥AB;
∴DE∥GH;
∴DE∥平面FGH,DE∩BE=E;
∴平面BDE∥平面FGH,BD平面BDE;
∴BD∥平面FGH;
(Ⅱ)连接HE,则HE∥CF;
∵CF⊥平面ABC;
∴HE⊥平面ABC,并且HG⊥HC;
∴HC,HG,HE三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设HC=1,则:
H(0,0,0),G(0,1,0),F(1,0,1),B(﹣1,0,0);
连接BG,根据已知条件BA=BC,G为AC中点;
∴BG⊥AC;
又CF⊥平面ABC,BG平面ABC;
∴BG⊥CF,AC∩CF=C;
∴BG⊥平面ACFD;
∴向量 ![]() 为平面ACFD的法向量;
为平面ACFD的法向量;
设平面FGH的法向量为 ![]() ,则:
,则: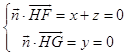 ,取z=1,则:
,取z=1,则: ![]() ;
;
设平面FGH和平面ACFD所成的锐二面角为θ,则:cosθ=|cos ![]() |=
|= ![]() ;
;
∴平面FGH与平面ACFD所成的角为60°
【解析】(Ⅰ)根据AB=2DE便可得到BC=2EF,从而可以得出四边形EFHB为平行四边形,从而得到BE∥HF,便有BE∥平面FGH,再证明DE∥平面FGH,从而得到平面BDE∥平面FGH,从而BD∥平面FGH;(Ⅱ)连接HE,根据条件能够说明HC,HG,HE三直线两两垂直,从而分别以这三直线为x,y,z轴,建立空间直角坐标系,然后求出一些点的坐标.连接BG,可说明 ![]() 为平面ACFD的一条法向量,设平面FGH的法向量为
为平面ACFD的一条法向量,设平面FGH的法向量为 ![]() ,根据
,根据 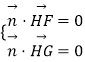 即可求出法向量
即可求出法向量 ![]() ,设平面FGH与平面ACFD所成的角为θ,根据cosθ=
,设平面FGH与平面ACFD所成的角为θ,根据cosθ= ![]() 即可求出平面FGH与平面ACFD所成的角的大小.
即可求出平面FGH与平面ACFD所成的角的大小.

【题目】为了解篮球爱好者小张的投篮命中率与打篮球时间之间的关系,下表记录了小张某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(1)求小张这![]() 天的平均投篮命中率;
天的平均投篮命中率;
(2)利用所给数据求小张每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的线性回归方程
之间的线性回归方程![]() ;(参考公式:
;(参考公式:![]() )
)
(3)用线性回归分析的方法,预测小李该月![]() 号打
号打![]() 小时篮球的投篮命中率.
小时篮球的投篮命中率.
【题目】2017年10月18日至24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级随机抽取的各100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图.
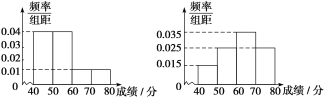
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;
(2)若称成绩在68分以上的学生知识渊博,试以上述数据估计该高一、高二两个年级学生的知识渊博率;
(3)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下,认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.
分类 | 成绩低于60分人数 | 成绩不低于60分人数 | 总计 |
高一年级 | |||
高二年级 | |||
总计 |
附:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
K2=![]() .
.