Question

【题目】如图，梯形中，∥，，，，将△沿对角线折起，设折起后点的位置为，使二面角为直二面角，给出下面四个命题：① ；②三棱锥的体积为；③平面；④平面平面；其中正确命题的个数是（ ）

A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

取BD中点O，根据面面垂直性质定理得平面，再根据线面垂直判定与性质定理、面面垂直判定定理证得平面以及平面平面；利用锥体体积公式求三棱锥的体积，最后根据反证法说明不成立.

因为，，所以为等腰直角三角形，

因为∥，，

所以,从而为等腰直角三角形，

取BD中点O，连接，如图，

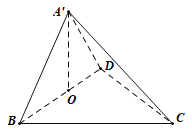
因为二面角为直二面角，所以平面平面，

因为为等腰直角三角形，所以平面平面,平面,因此平面，所以三棱锥的体积为,②正确；

因为平面，平面，所以，因为，,平面，所以平面；即③正确;

因为平面，平面；所以；由已知条件得,平面,因此平面,因为平面,所以平面平面；即④正确；

如果，而由平面，平面，所以，因为,平面，所以平面；因为平面；即,与矛盾,所以①不正确;

故选：C