МвДҝДЪИЭ
ЎҫМвДҝЎҝijѧУОӘөчІйёЯ¶юС§ЙъЙПѧ·іМЛщРиТӘөДКұјдЈЁөҘО»Јә·ЦЦУЈ©Ј¬ҙУёЯ¶юДкј¶С§ЙъЦРЛж»ъійИЎ![]() Гы°ҙЙПС§ЛщРиТӘКұјд·ЦЧйЈәөЪ
Гы°ҙЙПС§ЛщРиТӘКұјд·ЦЧйЈәөЪ![]() Чй
Чй![]() Ј¬өЪ
Ј¬өЪ![]() Чй
Чй![]() Ј¬өЪ
Ј¬өЪ![]() Чй
Чй![]() Ј¬өЪ
Ј¬өЪ![]() Чй
Чй![]() Ј¬өЪ
Ј¬өЪ![]() Чй
Чй![]() Ј¬өГөҪөДЖөВК·ЦІјЦұ·ҪНјИзНјЛщКҫЈ®
Ј¬өГөҪөДЖөВК·ЦІјЦұ·ҪНјИзНјЛщКҫЈ®
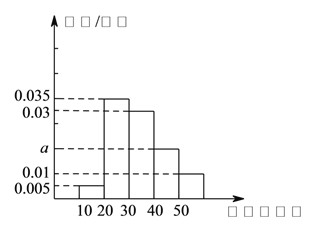
ЈЁ![]() Ј©ёщҫЭНјЦРКэҫЭЗу
Ј©ёщҫЭНјЦРКэҫЭЗу![]() өДЦөЈ®
өДЦөЈ®
ЈЁ![]() Ј©ИфҙУөЪ
Ј©ИфҙУөЪ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() ЧйЦРУГ·ЦІгійСщөД·Ҫ·ЁійИЎ
ЧйЦРУГ·ЦІгійСщөД·Ҫ·ЁійИЎ![]() ГыРВЙъІОУлҪ»НЁ°ІИ«ОКҫнөчІйЈ¬УҰҙУөЪ
ГыРВЙъІОУлҪ»НЁ°ІИ«ОКҫнөчІйЈ¬УҰҙУөЪ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() ЧйёчійИЎ¶аЙЩГыРВЙъЈҝ
ЧйёчійИЎ¶аЙЩГыРВЙъЈҝ
ЈЁ![]() Ј©ФЪЈЁ
Ј©ФЪЈЁ![]() Ј©өДМхјюПВЈ¬ёГРЈҫц¶ЁҙУХв
Ј©өДМхјюПВЈ¬ёГРЈҫц¶ЁҙУХв![]() ГыС§ЙъЦРЛж»ъійИЎ
ГыС§ЙъЦРЛж»ъійИЎ![]() ГыРВЙъІОјУҪ»НЁ°ІИ«Рыҙ«»о¶ҜЈ¬ЗуөЪ
ГыРВЙъІОјУҪ»НЁ°ІИ«Рыҙ«»о¶ҜЈ¬ЗуөЪ![]() ЧйЦБЙЩУРТ»ЦҫФёХЯұ»ійЦРөДёЕВКЈ®
ЧйЦБЙЩУРТ»ЦҫФёХЯұ»ійЦРөДёЕВКЈ®
Ўҫҙр°ёЎҝ(1) ![]() ;(2) ёчійИЎ
;(2) ёчійИЎ![]() ИЛЈ¬
ИЛЈ¬ ![]() ИЛЈ¬
ИЛЈ¬ ![]() ИЛ;(3)
ИЛ;(3) ![]() .
.
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©РЎҫШРОөДГж»эұнКҫҙЛЧйөДЖөВКЈ¬ёщҫЭЖөВКәНОӘ1ҝЙЗуөГ![]() өДЦөЎЈЈЁ2Ј©ПИЗуөЪ3Ўў4Ўў5ЧйөДЖөВКјҙЖөВК·ЦІјЦұ·ҪНјЦРёчЧйРЎҫШРОөДГж»эЈ¬ёщҫЭ
өДЦөЎЈЈЁ2Ј©ПИЗуөЪ3Ўў4Ўў5ЧйөДЖөВКјҙЖөВК·ЦІјЦұ·ҪНјЦРёчЧйРЎҫШРОөДГж»эЈ¬ёщҫЭ![]() ЗуөГёчЧйөДЖөКэЈ¬И»әуЗуөГҙЛ3ЧйөДЖөКэәНЎЈЧоәуёщҫЭұИАэјЖЛгёчЧйійИЎИЛКэЎЈЈЁ3Ј©јЗөЪ3ЧйөД3ГыРВЙъОӘ
ЗуөГёчЧйөДЖөКэЈ¬И»әуЗуөГҙЛ3ЧйөДЖөКэәНЎЈЧоәуёщҫЭұИАэјЖЛгёчЧйійИЎИЛКэЎЈЈЁ3Ј©јЗөЪ3ЧйөД3ГыРВЙъОӘ![]() ,өЪ4ЧйөД2ГыРВЙъОӘ
,өЪ4ЧйөД2ГыРВЙъОӘ![]() ,өЪ5ЧйөД1ГыРВЙъОӘ
,өЪ5ЧйөД1ГыРВЙъОӘ![]() Ј¬Ҫ«ҙУХв6ГыРВЙъЦРЛж»ъійИЎ2ГыЛщ°мә¬өД»щұҫКВјюТ»Т»АэҫЩІўөГөҪ»щұҫКВјюЧЬКэЈ¬ЖдЦРөЪ4ЧйЦБЙЩУРТ»ГыөД»щұҫКВјюФЩТ»Т»АэҫЩөГөҪҙЛКВјю°ьә¬өД»щұҫКВјюКэЎЈёщҫЭ№ЕөдёЕРНёЕВК№«КҪЗуЖдёЕВКЎЈ
Ј¬Ҫ«ҙУХв6ГыРВЙъЦРЛж»ъійИЎ2ГыЛщ°мә¬өД»щұҫКВјюТ»Т»АэҫЩІўөГөҪ»щұҫКВјюЧЬКэЈ¬ЖдЦРөЪ4ЧйЦБЙЩУРТ»ГыөД»щұҫКВјюФЩТ»Т»АэҫЩөГөҪҙЛКВјю°ьә¬өД»щұҫКВјюКэЎЈёщҫЭ№ЕөдёЕРНёЕВК№«КҪЗуЖдёЕВКЎЈ
ҪвЈәЈЁ1Ј©ТтОӘ![]() , 1·Ц
, 1·Ц
ЛщТФ![]() . 2·Ц
. 2·Ц
ЈЁ2Ј©ТАМвТвҝЙЦӘЈ¬
өЪ3ЧйөДИЛКэОӘ![]() Ј¬
Ј¬
өЪ4ЧйөДИЛКэОӘ![]() Ј¬
Ј¬
өЪ5ЧйөДИЛКэОӘ![]() .
.
ЛщТФ3Ўў4Ўў5ЧйИЛКэ№ІУР60. 3·Ц
ЛщТФАыУГ·ЦІгійСщөД·Ҫ·ЁФЪ60ГыС§ЙъЦРійИЎ6ГыРВЙъ,·ЦІгійСщөДійСщұИОӘ![]() 4·Ц
4·Ц
ЛщТФФЪөЪ3ЧйійИЎөДИЛКэОӘ![]() ИЛ Ј¬
ИЛ Ј¬
ФЪөЪ4ЧйійИЎөДИЛКэОӘ![]() ИЛЈ¬
ИЛЈ¬
ФЪөЪ5ЧйійИЎөДИЛКэОӘ![]() ИЛЈ¬ 7·Ц
ИЛЈ¬ 7·Ц
ЈЁ3Ј©јЗөЪ3ЧйөД3ГыРВЙъОӘ![]() ,өЪ4ЧйөД2ГыРВЙъОӘ
,өЪ4ЧйөД2ГыРВЙъОӘ![]() ,өЪ5ЧйөД1ГыРВЙъОӘ
,өЪ5ЧйөД1ГыРВЙъОӘ
![]()
![]() ,№ІУР15ЦЦ. 9·Ц
,№ІУР15ЦЦ. 9·Ц
ЖдЦРөЪ4ЧйөД2ГыРВЙъ![]() ЦБЙЩУРТ»ГыРВЙъұ»ійЦРөДУР:
ЦБЙЩУРТ»ГыРВЙъұ»ійЦРөДУР:
![]()
![]() №ІУР9ЦЦ, 11·Ц
№ІУР9ЦЦ, 11·Ц
ФтөЪ4ЧйЦБЙЩУРТ»ГыРВЙъұ»ійЦРөДёЕВКОӘ![]() 13·Ц
13·Ц

ЎҫМвДҝЎҝјЩЙи№ШУЪДіЙиұёөДК№УГДкПЮ![]() ЈЁДкЈ©әНЛщЦ§іцөДО¬РЮ·СУГ
ЈЁДкЈ©әНЛщЦ§іцөДО¬РЮ·СУГ![]() ЈЁНтФӘЈ©УРИзПВНіјЖЧКБПЈә
ЈЁНтФӘЈ©УРИзПВНіјЖЧКБПЈә
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
ИфУЙЧКБПЦӘЈ¬ ![]() ¶Ф
¶Ф![]() іКПЯРФПа№Ш№ШПөЈ¬КФЗуЈә
іКПЯРФПа№Ш№ШПөЈ¬КФЗуЈә
ЈЁ1Ј©»Ш№йЦұПЯ·ҪіМЈ»
ЈЁ2Ј©№АјЖК№УГДкПЮОӘ10ДкКұЈ¬О¬РЮ·СУГФјКЗ¶аЙЩЈҝ
ІОҝј№«КҪЈә»Ш№йЦұПЯ·ҪіМЈә ![]() .ЖдЦР
.ЖдЦР
ЈЁЧўЈә ![]() )
)
