题目内容
18.x,y满足约束条件$\left\{\begin{array}{l}x+2y-1≥0\\ x-y≥0\\ 0≤x≤k.\end{array}\right.$若z=x+ky的最小值为-2,则z的最大值为( )| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
分析 作出不等式组对应 的平面区域,利用数形结合即可求出k的值.
解答 解:显然k>0.联立$\left\{\begin{array}{l}x=k\\ x+2y-1=0\end{array}\right.$解得,$B(k,\frac{1-k}{2})$.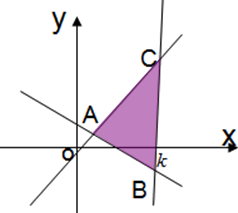
过点$B(k,\frac{1-k}{2})$时,直线$y=-\frac{1}{k}x+\frac{z}{k}$
在y轴上的截距最小,即$\frac{z}{k}$最小,
所以$k+k•\frac{1-k}{2}=-2$,解得k=4.
过点C(4,4)时,z=x+4y取最大值20.
故选:C
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合是解决本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.已知集合A={-2,3},B={x|x≤2},U=A∪B,则∁U(A∩B)=( )
| A. | {3} | B. | {x|x≤2,或x=3} | ||
| C. | {x|x<-2或-2<x≤2,或x=3} | D. | {x|x<-2,或-2<x≤2} |
3.某单位要从甲、乙、丙、丁四支门球队中选拔两支参加上级比赛,选拔赛采用单循环制(即每两个队比赛一场),并规定积分前两名的队出线,其中胜一场积3分,平一场积1分,负一场积0分.在经过三场比赛后,目前的积分状况如下:甲队积7分,乙队积1分,丙和丁队各积0分.根据以往的比赛情况统计:
注:各队之间比赛结果相互独立.
(Ⅰ)选拔赛结束,求乙队积4分的概率;
(Ⅱ)设随机变量X为选拔赛结束后乙队的积分,求随机变量X的分布列与数学期望;
(Ⅲ)在目前的积分情况下,M同学认为:乙队至少积4分才能确保出线,N同学认为:乙队至少积5分才能确保出线.你认为谁的观点对?或是两者都不对?(直接写结果,不需证明)
| 乙队胜的概率 | 乙队平的概率 | 乙队负的概率 | |
| 与丙 队比赛 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 与丁队比赛 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
(Ⅰ)选拔赛结束,求乙队积4分的概率;
(Ⅱ)设随机变量X为选拔赛结束后乙队的积分,求随机变量X的分布列与数学期望;
(Ⅲ)在目前的积分情况下,M同学认为:乙队至少积4分才能确保出线,N同学认为:乙队至少积5分才能确保出线.你认为谁的观点对?或是两者都不对?(直接写结果,不需证明)
10.设集合M={x∈R|y=$\sqrt{x+1}$},N={y∈R|y=x2-1,x∈R},则集合M和N的关系是( )
| A. | M=N | B. | M∪N=R | C. | N?M | D. | M?N |
 如图,边长为2的正方形ABCD是圆柱的中截面,点E为线段BC的中点,点S为圆柱的下底面圆周上异于A,B的一个动点.
如图,边长为2的正方形ABCD是圆柱的中截面,点E为线段BC的中点,点S为圆柱的下底面圆周上异于A,B的一个动点. 如图,在等腰梯形ABCD中,AB∥CD,AD=CD=CB=1,∠ABC=60°,四边形ACEF为矩形,且AF⊥AB,CE=1.
如图,在等腰梯形ABCD中,AB∥CD,AD=CD=CB=1,∠ABC=60°,四边形ACEF为矩形,且AF⊥AB,CE=1.