题目内容
9.某商场根据市场调研,决定从3种服装商品、2种家电商品和4种日用商品中选出3种商品进行促销活动.(Ⅰ)求选出的3种商品中至少有一种日用商品的概率;
(Ⅱ)被选中的促销商品在现价的基础上提高60元进行销售,同时提供3次抽奖的机会,第一次和第二次中奖均可获得奖金40元,第三次中奖可获得奖金30元,假设顾客每次抽奖时中奖与否是等可能的,顾客所得奖金总数为X元,求随机变量X的分布列和数学期望.
分析 (I)设选出的3种商品中至少有一种是日用商品为事件A,利用间接法能求出选出的3种商品中至少有一种是日用商品的概率.
(Ⅱ)设顾客抽奖的中奖奖金总额为X,则X的可能取值为0,30,40,80,70,110分别求出P(X=0),P(X=30),P(X=40),P(X=80),P(X=70),P(X=110),由此能求出顾客中奖次数的数学期望EX.
解答 解:(I)从3种服装商品、2种家电商品,4种日用商品中,选出3种商品,一共有${C}_{9}^{3}$种不同的选法,选出的3种商品中,没有日用商品的选法有${C}_{5}^{3}$种.
所以选出的3种商品至少有一种日用商品的概率为P=1-$\frac{{C}_{5}^{3}}{{C}_{9}^{3}}=\frac{37}{42}$.
(Ⅱ)X可能取得值为0,30,40,70,80,110
P(X=0)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\frac{1}{8}$
P(X=30)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\frac{1}{8}$
P(X=40)=${C}_{2}^{1}(\frac{1}{2})^{2}×\frac{1}{2}=\frac{1}{4}$
P(X=70)=${C}_{2}^{1}(\frac{1}{2})^{2}×\frac{1}{2}=\frac{1}{4}$
P(X=80)=$(\frac{1}{2})^{2}×\frac{1}{2}=\frac{1}{8}$
P(X=110)=$(\frac{1}{2})^{2}×\frac{1}{2}=\frac{1}{8}$
所以X的分布列为
| X | 0 | 30 | 40 | 70 | 80 | 110 |
| P | $\frac{1}{8}$ | $\frac{1}{8}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{8}$ |
点评 本题主要考查超几何分布的应用和随机变量的分布列期望,属中档题型,高考常考题型.

| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
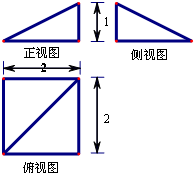
| A. | $\frac{9}{2}$πcm3 | B. | 36πcm3 | C. | $\frac{64}{3}$πcm3 | D. | 9πcm3 |
 如图,曲线C1:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1(y≤0);曲线C2:x2=4y,自曲线C1上一点A作C2的两条切线,切点分别为B,C.
如图,曲线C1:$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1(y≤0);曲线C2:x2=4y,自曲线C1上一点A作C2的两条切线,切点分别为B,C.