题目内容
10.以下四个关于圆锥曲线的命题中:A.设A、B为两个定点,k为非零常数,|$\overrightarrow{PA}$|-|$\overrightarrow{PB}$|=k,则动点P的轨迹为双曲线
B.过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$),则动点P的轨迹为圆
C.0<θ<$\frac{π}{4}$,则双曲线C1:$\frac{{x}^{2}}{co{s}^{2}θ}$-$\frac{{y}^{2}}{si{n}^{2}θ}$=1与C2:$\frac{{y}^{2}}{si{n}^{2}θ}$-$\frac{{x}^{2}}{si{n}^{2}θta{n}^{2}θ}$=1的离心率相同
D.已知两定点F1(-1,0),F2(1,0)和一动点P,若|PF1|•|PF2|=a2(a≠0),则点P的轨迹关于原点对称
其中真命题的序号为B.C.D(写出所有真命题的序号)
分析 A.利用双曲线的定义判断正误即可;
B.定圆C和定点A具体化,利用向量间的关系求出点B和点P的坐标间的关系,再利用B在圆上就可求出动点P的轨迹,然后在下结论即可.
C.求出离心率,即可判断;
D.化简整理,即可分析其正误.
解答 解:A.若动点P的轨迹为双曲线,则|k|要小于A、B为两个定点间的距离.当|k|大于A、B为两个定点间的距离时动点P的轨迹不是双曲线.故A错误,
B.设定圆C的方程为x2+y2=9,点A(3,0),B(a,b),点P(x,y),
则由$\overrightarrow{OP}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$得动点P为动弦AB的中点,所以有$\left\{\begin{array}{l}{x=\frac{a+3}{2}}\\{y=\frac{b}{2}}\end{array}\right.$⇒$\left\{\begin{array}{l}{a=2x-3}\\{b=2y}\end{array}\right.$
又因为点B在圆上所以有(2x-3)2+(2y)2=9,即(x-$\frac{3}{2}$)2+y2=$\frac{9}{4}$,即动点P的轨迹为圆.故B正确,
C.若0<θ<$\frac{π}{4}$,则双曲线C1:$\frac{x^2}{{{{cos}^2}θ}}-\frac{y^2}{{{{sin}^2}θ}}$=1中,a=cosθ,b=sinθ,c=1,则离心率为$\frac{c}{a}=\frac{1}{cosθ}$
C2:$\frac{y^2}{{{{sin}^2}θ}}-\frac{x^2}{{{{sin}^2}θ{{tan}^2}θ}}$=1中,a=sinθ,b=sinθtanθ,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{si{n}^{2}θ+si{n}^{2}θta{n}^{2}θ}$=tanθ,则离心率为$\frac{c}{a}$=$\frac{tanθ}{sinθ}$=$\frac{1}{cosθ}$,则离心率相同,故C正确;
D.设P(x,y)为曲线|PF1|•|PF2|=$\sqrt{(x+1)^{2}+{y}^{2}}$•$\sqrt{(x-1)^{2}+{y}^{2}}$=a2(a≠0)上任意一点,
则P(x,y)关于原点(0,0)的对称点为P′(-x,-y),
∵$\sqrt{(-x+1)^{2}+(-y)^{2}}$•$\sqrt{(-x-1)^{2}+(-y)^{2}}$=$\sqrt{(x-1)^{2}+{y}^{2}}$•$\sqrt{(x+1)^{2}+{y}^{2}}$=a2(a≠0),
即P′(-x,-y)也在曲线$\sqrt{(x+1)^{2}+{y}^{2}}$•$\sqrt{(x-1)^{2}+{y}^{2}}$=a2(a≠0)上,
∴点P的轨迹曲线$\sqrt{(x+1)^{2}+{y}^{2}}$•$\sqrt{(x-1)^{2}+{y}^{2}}$=a2(a≠0)关于原点对称,故D正确,
故答案为:B.C.D
点评 本题考查命题的真假判断与应用,着重考查圆锥曲线的概念及应用,考查转化思想与运算能力,属于中档题.

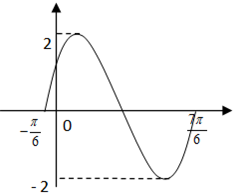
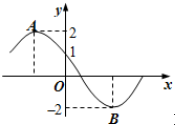
| A. | y=2sin($\frac{x}{2}$-$\frac{π}{6}$) | B. | y=2sin($\frac{x}{2}$+$\frac{5π}{12}$) | C. | y=-2sin($\frac{3x}{2}$-$\frac{3π}{4}$) | D. | $y=-2sin(\frac{3x}{2}+\frac{π}{4})$ |
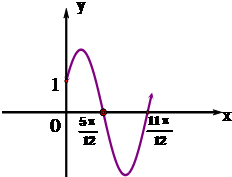 (1)已知$f(x)=Asin({ωx+φ})({x∈R,ω>0,0<φ<\frac{π}{2}})$的部分图象如下图,求f(x)的解析式;
(1)已知$f(x)=Asin({ωx+φ})({x∈R,ω>0,0<φ<\frac{π}{2}})$的部分图象如下图,求f(x)的解析式;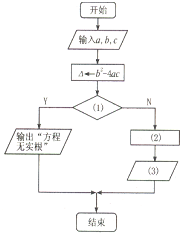 如图是求解一元二次方程ax2+bx+c=0(a≠0)的流程图,根据题意填写:
如图是求解一元二次方程ax2+bx+c=0(a≠0)的流程图,根据题意填写: