题目内容
18.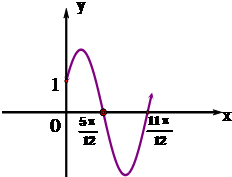 (1)已知$f(x)=Asin({ωx+φ})({x∈R,ω>0,0<φ<\frac{π}{2}})$的部分图象如下图,求f(x)的解析式;
(1)已知$f(x)=Asin({ωx+φ})({x∈R,ω>0,0<φ<\frac{π}{2}})$的部分图象如下图,求f(x)的解析式;(2)若$f(x)=tan({ωx+\frac{π}{4}})({ω>0})$且f(x)在$({-\frac{π}{3},\frac{π}{2}})$上为单调递增函数,求ω的最大值.
分析 (1)由周期求出ω,由五点法作图求出φ的值,根据特殊点的坐标求出A的值,可得函数的解析式.
(2)根据正切函数的单调性求得函数f(x)的增区间,再根据f(x)在$({-\frac{π}{3},\frac{π}{2}})$上为单调递增函数,可得 $({-\frac{π}{3},\frac{π}{2}})$⊆($\frac{kπ}{ω}$-$\frac{3π}{4ω}$,$\frac{kπ}{ω}$+$\frac{π}{4ω}$),k∈Z,可得$\left\{\begin{array}{l}{-\frac{3π}{4ω}≤-\frac{π}{3}}\\{\frac{π}{4ω}≥\frac{π}{2}}\end{array}\right.$,由此求得ω的最大值.
解答 解:(1)由函数f(x)的图象可得$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{11π}{12}$-$\frac{5π}{12}$,∴ω=2.
再根据五点法作图,可得2×$\frac{5π}{12}$+φ=π,求得φ=$\frac{π}{6}$,故f(x)=Asin(2x+$\frac{π}{6}$).
再根据函数的图象经过点(0,1),可得Asin$\frac{π}{6}$=1,求得 A=2,∴f(x)=2sin(2x+$\frac{π}{6}$).
(2)对于 $f(x)=tan({ωx+\frac{π}{4}})({ω>0})$,令kπ-$\frac{π}{2}$<ωx+$\frac{π}{4}$<kπ+$\frac{π}{2}$,k∈Z,求得$\frac{kπ}{ω}$-$\frac{3π}{4ω}$<x<$\frac{kπ}{ω}$+$\frac{π}{4ω}$,
可得函数f(x)的增区间为($\frac{kπ}{ω}$-$\frac{3π}{4ω}$,$\frac{kπ}{ω}$+$\frac{π}{4ω}$),k∈Z.
结合f(x)在$({-\frac{π}{3},\frac{π}{2}})$上为单调递增函数,可得 $({-\frac{π}{3},\frac{π}{2}})$⊆($\frac{kπ}{ω}$-$\frac{3π}{4ω}$,$\frac{kπ}{ω}$+$\frac{π}{4ω}$),k∈Z.
∴$\left\{\begin{array}{l}{-\frac{3π}{4ω}≤-\frac{π}{3}}\\{\frac{π}{4ω}≥\frac{π}{2}}\end{array}\right.$,求得ω≤$\frac{1}{2}$,故ω的最大值为$\frac{1}{2}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,根据特殊点的坐标求出A的值.还考查正切函数的单调性,属于基础题.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | 20 | B. | 60 | C. | 160 | D. | 240 |
| A. | $\frac{31}{81}$ | B. | $\frac{11}{27}$ | C. | $\frac{16}{27}$ | D. | $\frac{50}{81}$ |
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{3}{2}$ |
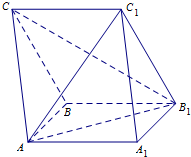 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.
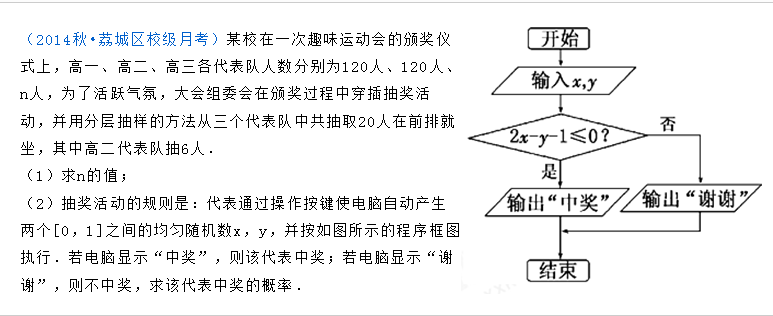
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.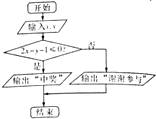 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人,120人,n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从第三个代表队中共抽取20人在前排就坐参与抽奖,其中高二代表队有6人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人,120人,n人,为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从第三个代表队中共抽取20人在前排就坐参与抽奖,其中高二代表队有6人.