题目内容
15.在△ABC中,sin2C≤(sinA-sinB)2+sinAsinB,则C的取值范围是( )| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,π) |
分析 利用正弦定理化简已知的不等式,再利用余弦定理表示出cosC,将得出的不等式变形后代入表示出的cosC中,得出cosC的范围,由C为三角形的内角,根据余弦函数的图象与性质即可求出C的取值范围.
解答 解:利用正弦定理化简sin2C≤(sinA-sinB)2+sinAsinB,
即sin2C≤sin2A+sin2B-sinAsinB,
得:c2≤a2+b2-ab,
变形得:b2+a2-c2≥ab,
∴cosC=$\frac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab}$≥$\frac{ab}{2ab}$=$\frac{1}{2}$,
又C为三角形的内角,
则C的取值范围是(0,$\frac{π}{3}$].
故选C.
点评 此题考查了正弦、余弦定理,特殊角的三角函数值,以及余弦函数的图象与性质,熟练掌握正弦、余弦定理是解本题的关键.

练习册系列答案
相关题目
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=10,b=8,B=30°,那么△ABC的解的情况是( )
| A. | 无解 | B. | 一解 | C. | 两解 | D. | 一解或两解 |
3.已知直线x+2ay-1=0与直线(a-2)x-ay+2=0平行,则a的值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{2}$或0 | C. | -$\frac{2}{3}$ | D. | -$\frac{2}{3}$或0 |
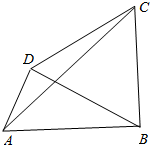 如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.
如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.