题目内容
9.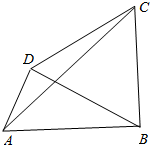 如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.
如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.(1)当∠BAD=$\frac{π}{3}$时,设$\overrightarrow{AC}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,求x,y的值;
(2)设∠BAD=α,则当α为多少时,四边形ABCD的面积S最大,并求出最大值.
分析 (1)过点C作CE∥AD交AB于点E,在△BCE中,BC=$\sqrt{3}$,∠ABC=$\frac{π}{2}$,CE=2,BE=1,AE=1,可得$\overrightarrow{AC}$=$\overrightarrow{AE}$+$\overrightarrow{EC}$=$\frac{1}{2}$$\overrightarrow{AB}$+2$\overrightarrow{AD}$,即可求x,y的值;
(2)求出BD,表示出面积,即可求得四边形ABCD的面积S最大.
解答  解:(1)在△ABD中,∵AB=2,AD=1,∠BAD=$\frac{π}{3}$,
解:(1)在△ABD中,∵AB=2,AD=1,∠BAD=$\frac{π}{3}$,
∴BD=$\sqrt{3}$,∠ABD=$\frac{π}{6}$,∠ADB=$\frac{π}{2}$,∠ABC=$\frac{π}{2}$,∠ADC=$\frac{5π}{6}$,
过点C作CE∥AD交AB于点E,在△BCE中,BC=$\sqrt{3}$,∠ABC=$\frac{π}{2}$,
∴CE=2,BE=1,
∴AE=1,
∴$\overrightarrow{AC}$=$\overrightarrow{AE}$+$\overrightarrow{EC}$=$\frac{1}{2}$$\overrightarrow{AB}$+2$\overrightarrow{AD}$,
∴x=$\frac{1}{2}$,y=2;
(2)在△ABD中,由余弦定理可得BD=$\sqrt{5-4cosα}$,
∴S△ABD=sinα,S△BDC=$\frac{\sqrt{3}}{4}B{D}^{2}$=$\frac{\sqrt{3}}{4}$(5-4cosα),
∴S=sinα-$\sqrt{3}$cosα+$\frac{5\sqrt{3}}{4}$=2sin(α-$\frac{π}{3}$)+$\frac{5\sqrt{3}}{4}$,α∈(0,π),
∴Smax=2+$\frac{5\sqrt{3}}{4}$,此时α=$\frac{5π}{6}$.
点评 本题考查向量在几何中的运用,考查余弦定理,考查学生分析解决问题的能力,属于中档题.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,π) |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{7π}{12}$ | |||
| Asin(ωx+φ) | 0 | -5 |
(Ⅱ)将y=f(x)图象上所有点向左平行移动$\frac{π}{6}$个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.