题目内容
11.某校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩,数学成绩分组及各组频数如下:[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.(Ⅰ)估计成绩在80分以上学生的比例;
(Ⅱ)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学,已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
分析 (I)先求出成绩在[80,100)的学生数,再结合题意,计算可得答案;
(Ⅲ)根据题意,记成绩在[40,50)上的2名学生为a、甲,在[90,100)内的4名学生记为1、2、3、乙,列举“二帮一”的全部情况,可得其情况数目与甲乙两名同学恰好在同一小组的情况数目,由古典概型公式,计算可得答案
解答 解:(Ⅰ)由频率分布表可得,成绩在[80,100)的学生数为12+4=16,
则成绩在80分以上的学生的比例为P1=$\frac{16}{50}$=32%,
(Ⅱ)记成绩在[40,50)上的2名学生为a、甲,在[90,100)内的4名学生记为1、2、3、乙,
则选取的情况有:
(1,2,a)、(1,2,甲)、(1,3,a)、(1,3,甲)、
(1,乙,a)、(1,乙,甲)、(2,3,a)、(2,3,甲)、
(2,乙,a)、(2,乙,甲)、(3,乙,a)、(3,乙,甲),共12种;
其中甲乙两名同学恰好在同一小组的情况有3种,
则甲、乙两同学恰好被安排在同一小组的概率P2=$\frac{3}{12}$=$\frac{1}{4}$.
点评 本题考查古典概型的计算与频率分布表的作法,关键是运用表中的数据,正确做出频率分布表.

练习册系列答案
相关题目
18.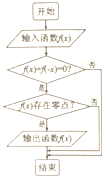 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数:
①f(x)=sinx
②f(x)=cosx
③f(x)=$\frac{1}{x}$
④f(x)=log2x
则输出的函数是( )
 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx
②f(x)=cosx
③f(x)=$\frac{1}{x}$
④f(x)=log2x
则输出的函数是( )
| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=log2x |
15.在△ABC中,sin2C≤(sinA-sinB)2+sinAsinB,则C的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,π) |
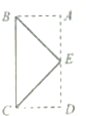 如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π.
如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π.