题目内容
5.函数y=$\sqrt{lo{g}_{\frac{1}{2}}4x-2}$的定义域是(0,$\frac{1}{16}$].分析 欲求函数的定义域,只需找到使函数解析式有意义的x的取值范围,因为函数中有对数,所以真数大于0,因为函数中有二次根式,所以被开方数大于等于0,解不等式组即可.
解答 解:要使函数有意义,需满足$\left\{\begin{array}{l}{lo{{g}_{\frac{1}{2}}}^{4x-2}≥0}\\{4x-2>0}\end{array}\right.$,
解得0<x≤$\frac{1}{16}$,
∴函数的定义域为(0,$\frac{1}{16}$].
故答案为(0,$\frac{1}{16}$].
点评 本题主要考察了函数定义域的求法,主要是求使函数成立的x的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知f(x+1)=lgx,则函数f(2x-1)的定义域为( )
| A. | (-1,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (2,+∞) |
14.一个边长为6的正方形铁片,铁片的四角截去四个边长均为x的小正方形,然后做成一个无盖方盒.当无盖方盒的容积V最大时,x的值为( )
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{6}$ |
15.在△ABC中,sin2C≤(sinA-sinB)2+sinAsinB,则C的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,π) |
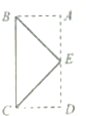 如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π.
如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π.