题目内容
已知f(x)=x3+mx2-x+2(m∈R)
如果函数的单调减区间恰为(-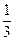 ,1),求函数f(x)的解析式;
,1),求函数f(x)的解析式;
(2)若f(x)的导函数为f '(x),对任意x∈(0,+∞),不等式f '(x)≥2xlnx-1恒成立,求实数m的取值范围.
如果函数的单调减区间恰为(-
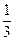 ,1),求函数f(x)的解析式;
,1),求函数f(x)的解析式;(2)若f(x)的导函数为f '(x),对任意x∈(0,+∞),不等式f '(x)≥2xlnx-1恒成立,求实数m的取值范围.
(1)f(x)=x3-x2-x+2
(2)m的取值范围是[ln2-ln3e,+∞).
(2)m的取值范围是[ln2-ln3e,+∞).
(1)f '(x)=3x2+2mx-1,
由题意,f '(x)=3x2+2mx-1<0的解集是(-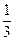 ,1),
,1),
即3x2+2mx-1=0的两根分别为-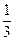 ,1,将x=1或-
,1,将x=1或-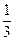 代入方程3x2+2mx-1=0得m=-1,
代入方程3x2+2mx-1=0得m=-1,
∴f(x)=x3-x2-x+2,
(2)由题意知3x2+2mx-1≥2xlnx-1在x∈(0,+∞)恒成立,
即m≥lnx-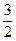 x在x∈(0,+∞)恒成立,
x在x∈(0,+∞)恒成立,
设h(x)=lnx-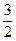 x,则h'(x)=
x,则h'(x)=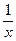 -
-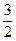 ,
,
令h'(x)=0得x=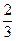 ,
,
当0<x<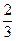 时,h'(x)>0;当x>
时,h'(x)>0;当x>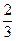 时,h'(x)<0,
时,h'(x)<0,
∴当x=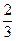 时,h(x)取得最大值为ln
时,h(x)取得最大值为ln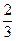 -1=ln2-ln3e,
-1=ln2-ln3e,
表明m≥ln2-ln3e,
因此m的取值范围是[ln2-ln3e,+∞).
由题意,f '(x)=3x2+2mx-1<0的解集是(-
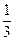 ,1),
,1),即3x2+2mx-1=0的两根分别为-
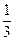 ,1,将x=1或-
,1,将x=1或-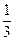 代入方程3x2+2mx-1=0得m=-1,
代入方程3x2+2mx-1=0得m=-1,∴f(x)=x3-x2-x+2,
(2)由题意知3x2+2mx-1≥2xlnx-1在x∈(0,+∞)恒成立,
即m≥lnx-
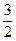 x在x∈(0,+∞)恒成立,
x在x∈(0,+∞)恒成立,设h(x)=lnx-
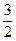 x,则h'(x)=
x,则h'(x)=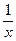 -
-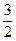 ,
,令h'(x)=0得x=
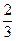 ,
,当0<x<
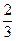 时,h'(x)>0;当x>
时,h'(x)>0;当x>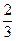 时,h'(x)<0,
时,h'(x)<0,∴当x=
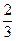 时,h(x)取得最大值为ln
时,h(x)取得最大值为ln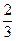 -1=ln2-ln3e,
-1=ln2-ln3e,表明m≥ln2-ln3e,
因此m的取值范围是[ln2-ln3e,+∞).

练习册系列答案
相关题目
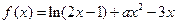 在
在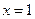 处取得极值.
处取得极值.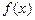 的单调区间;
的单调区间;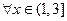 ,
,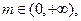
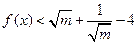 .
.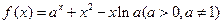 .(Ⅰ)当
.(Ⅰ)当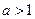 时,求证:函数
时,求证:函数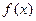 在
在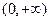 上单调递增;(Ⅱ)若函数
上单调递增;(Ⅱ)若函数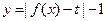 有三个零点,求
有三个零点,求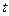 的值;
的值;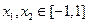 ,使得
,使得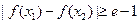 ,试求
,试求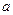 的取值范围.
的取值范围.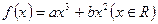 的图像过点P(-1,2),且在点P处的切线恰好与直线
的图像过点P(-1,2),且在点P处的切线恰好与直线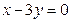 垂直。
垂直。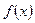 的解析式;
的解析式;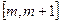 上单调递增,求实数m的取值范围。
上单调递增,求实数m的取值范围。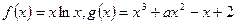
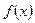 的单调区间;
的单调区间;
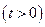 上的最小值;
上的最小值;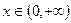 ,
,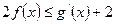 恒成立,求实数
恒成立,求实数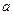 的取值范围.
的取值范围. 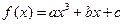
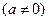 为奇函数,其图象在点
为奇函数,其图象在点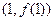 处的切线与直线
处的切线与直线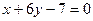 垂直,且在x=-1处取得极值.
垂直,且在x=-1处取得极值.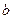 ,
,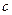 的值;
的值;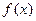 在
在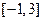 上的最大值和最小值。
上的最大值和最小值。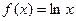 ,
,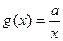 ,设
,设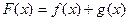 .
.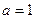 时,求函数
时,求函数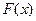 的单调区间;
的单调区间;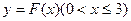 图象上任意一点
图象上任意一点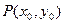 为切点的切线斜率
为切点的切线斜率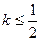 恒成立,求实数
恒成立,求实数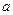 的最小值.
的最小值. 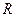 上的奇函数
上的奇函数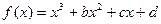 在
在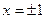 处取得极值.
处取得极值.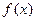 的解析式;
的解析式;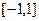 上任意两个自变量的值
上任意两个自变量的值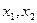 ,都有
,都有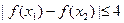 成立;
成立;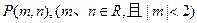 可作曲线
可作曲线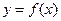 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.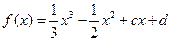 有极值.
有极值.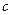 的取值范围;
的取值范围;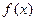 在
在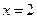 处取得极值,且当
处取得极值,且当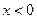 时,
时,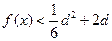 恒成立,求
恒成立,求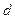 的取值范围.
的取值范围.