题目内容
(本小题满分16分)已知函数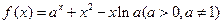 .(Ⅰ)当
.(Ⅰ)当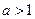 时,求证:函数
时,求证:函数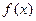 在
在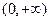 上单调递增;(Ⅱ)若函数
上单调递增;(Ⅱ)若函数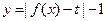 有三个零点,求
有三个零点,求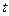 的值;
的值;
(Ⅲ)若存在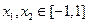 ,使得
,使得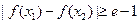 ,试求
,试求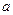 的取值范围.
的取值范围.
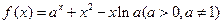 .(Ⅰ)当
.(Ⅰ)当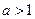 时,求证:函数
时,求证:函数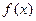 在
在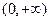 上单调递增;(Ⅱ)若函数
上单调递增;(Ⅱ)若函数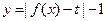 有三个零点,求
有三个零点,求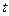 的值;
的值;(Ⅲ)若存在
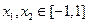 ,使得
,使得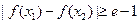 ,试求
,试求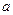 的取值范围.
的取值范围.(Ⅰ)见解析 (Ⅱ) 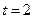 (Ⅲ)
(Ⅲ)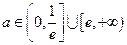
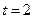 (Ⅲ)
(Ⅲ)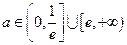
(Ⅰ)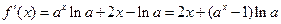 …3分
…3分
由于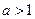 ,故当
,故当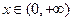 时,
时,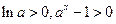 ,所以
,所以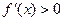 ,
,
故函数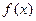 在
在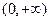 上单调递增……5分
上单调递增……5分
(Ⅱ)当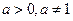 时,因为
时,因为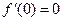 ,且
,且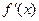 在R上单调递增,故
在R上单调递增,故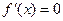 有唯一解
有唯一解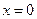 所以
所以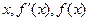 的变化情况如下表所示:
的变化情况如下表所示:
又函数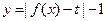 有三个零点,所以方程
有三个零点,所以方程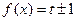 有三个根,
有三个根,
而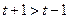 ,所以
,所以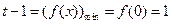 ,解得
,解得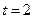 …11分
…11分
(Ⅲ)因为存在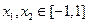 ,使得
,使得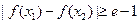 ,
,
所以当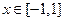 时,
时,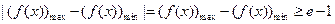 …………12分
…………12分
由(Ⅱ)知,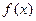 在
在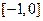 上递减,在
上递减,在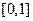 上递增,
上递增,
所以当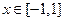 时,
时,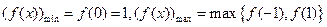 ,
,
而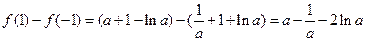 ,
,
记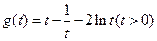 ,因为
,因为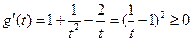 (当
(当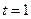 时取等号),
时取等号),
所以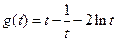 在
在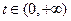 上单调递增,而
上单调递增,而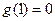 ,
,
所以当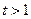 时,
时,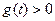 ;当
;当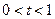 时,
时,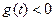 ,
,
也就是当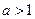 时,
时,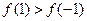 ;当
;当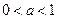 时,
时,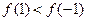 ………………………14分
………………………14分
①当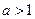 时,由
时,由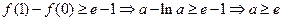 ,
,
②当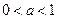 时,由
时,由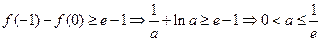 ,
,
综上知,所求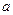 的取值范围为
的取值范围为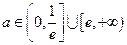 ………16分
………16分
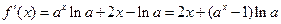 …3分
…3分由于
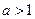 ,故当
,故当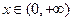 时,
时,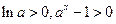 ,所以
,所以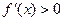 ,
,故函数
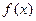 在
在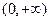 上单调递增……5分
上单调递增……5分(Ⅱ)当
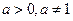 时,因为
时,因为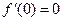 ,且
,且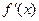 在R上单调递增,故
在R上单调递增,故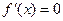 有唯一解
有唯一解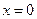 所以
所以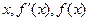 的变化情况如下表所示:
的变化情况如下表所示:| x | 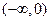 | 0 | 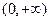 |
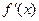 | - | 0 | + |
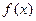 | 递减 | 极小值 | 递增 |
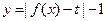 有三个零点,所以方程
有三个零点,所以方程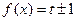 有三个根,
有三个根,而
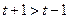 ,所以
,所以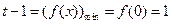 ,解得
,解得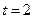 …11分
…11分(Ⅲ)因为存在
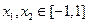 ,使得
,使得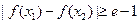 ,
,所以当
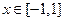 时,
时,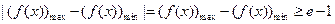 …………12分
…………12分由(Ⅱ)知,
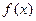 在
在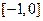 上递减,在
上递减,在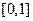 上递增,
上递增,所以当
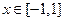 时,
时,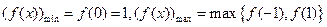 ,
,而
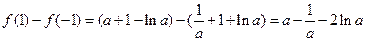 ,
,记
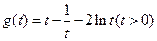 ,因为
,因为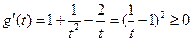 (当
(当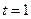 时取等号),
时取等号),所以
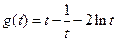 在
在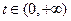 上单调递增,而
上单调递增,而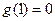 ,
,所以当
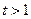 时,
时,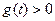 ;当
;当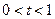 时,
时,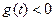 ,
,也就是当
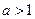 时,
时,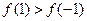 ;当
;当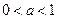 时,
时,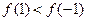 ………………………14分
………………………14分①当
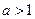 时,由
时,由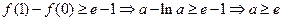 ,
,②当
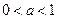 时,由
时,由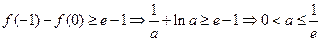 ,
,综上知,所求
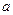 的取值范围为
的取值范围为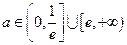 ………16分
………16分
练习册系列答案
相关题目
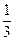 ,1),求函数f(x)的解析式;
,1),求函数f(x)的解析式;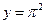 ,则
,则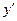 等于( )
等于( )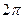
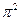
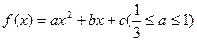 的图象经过A(0,1),且在该点处的切线与直线
的图象经过A(0,1),且在该点处的切线与直线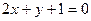 平行.
平行.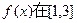 上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.
上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.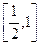 上变化时,证明:
上变化时,证明: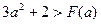
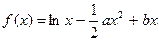
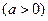 且
且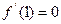 .
.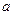 式子表示
式子表示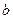 ;(Ⅱ)求
;(Ⅱ)求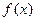 的单调区间;(Ⅲ)若
的单调区间;(Ⅲ)若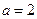 ,试求
,试求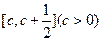 上的最大值.
上的最大值.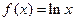 ,
,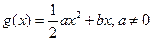 。
。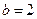 ,且函数
,且函数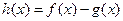 存在单调递减区间,求
存在单调递减区间,求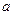 的取值范围;
的取值范围;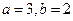 时,求函数
时,求函数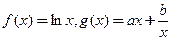 ,它们的图象在
,它们的图象在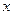 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当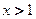 时,
时,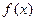 与
与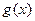 的大小关系是 ( )
的大小关系是 ( )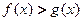
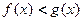

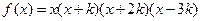 ,且
,且 ,则
,则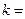

 ,求
,求 .
.