题目内容
已知F1,F2分别是椭圆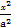 +
+ =1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .
=1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .
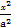 +
+ =1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .
=1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .e=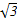 -1
-1
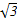 -1
-1因为△F2AB是等边三角形,所以A(- ,
,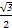 c)在椭圆
c)在椭圆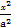 +
+ =1上,所以
=1上,所以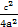 +
+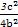 =1,因为c2=a2-b2,所以,4a4-8a2c2+c4=0,即e4-8e2+4=0,
=1,因为c2=a2-b2,所以,4a4-8a2c2+c4=0,即e4-8e2+4=0,
所以,e2=4±2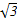 ,e=
,e=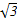 -1或e=
-1或e=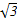 +1(舍).
+1(舍).
【误区警示】本题易出现答案为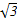 -1或
-1或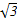 +1的错误,其错误原因是没有考虑椭圆离心率的范围.
+1的错误,其错误原因是没有考虑椭圆离心率的范围.
 ,
,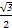 c)在椭圆
c)在椭圆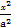 +
+ =1上,所以
=1上,所以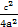 +
+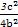 =1,因为c2=a2-b2,所以,4a4-8a2c2+c4=0,即e4-8e2+4=0,
=1,因为c2=a2-b2,所以,4a4-8a2c2+c4=0,即e4-8e2+4=0,所以,e2=4±2
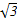 ,e=
,e=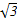 -1或e=
-1或e=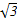 +1(舍).
+1(舍).【误区警示】本题易出现答案为
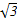 -1或
-1或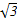 +1的错误,其错误原因是没有考虑椭圆离心率的范围.
+1的错误,其错误原因是没有考虑椭圆离心率的范围.
练习册系列答案
相关题目
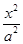 +
+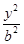 =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.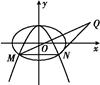
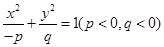 表示双曲线,那么下列椭圆中,与这个双曲线共焦点的是( )
表示双曲线,那么下列椭圆中,与这个双曲线共焦点的是( )


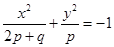
 +
+ =1(a>b>0)的右顶点为A(1,0),过其焦点且垂直长轴的弦长为1,则椭圆方程为 .
=1(a>b>0)的右顶点为A(1,0),过其焦点且垂直长轴的弦长为1,则椭圆方程为 .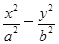 =1和椭圆
=1和椭圆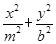 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( ) +
+ =1
=1 +
+ =1
=1 =1
=1 =1
=1