题目内容
已知椭圆的中心为坐标原点,短轴长为2,一条准线的方程为l:x=2.
(1)求椭圆的标准方程.
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
(1)求椭圆的标准方程.
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
(1) 
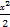+y2=1 (2)见解析
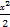+y2=1 (2)见解析(1)∵椭圆C的短轴长为2,椭圆C的一条准线为l:x=2,
∴不妨设椭圆C的方程为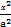
+y2=1.
∴
=
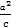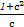=2,即c=1.
∴椭圆C的方程为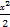+y2=1.
(2)F(1,0),右准线为l:x=2.设N(x0,y0),
则直线FN的斜率为kFN=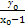
,直线ON的斜率为kON=
.
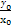∵FN⊥OM,∴直线OM的斜率为kOM=-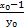
.
∴直线OM的方程为y=-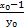x,
点M的坐标为M(2,-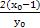
).
∴直线MN的斜率为kMN=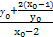
.
∵MN⊥ON,∴kMNkON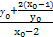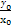=-1.
∴·=-1.
∴
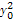+2(x0-1)+x0(x0-2)=0,即
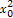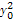+=2.
∴ON=
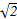为定值.
∴不妨设椭圆C的方程为
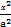+y2=1.∴
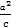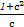==2,即c=1.∴椭圆C的方程为
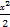+y2=1.(2)F(1,0),右准线为l:x=2.设N(x0,y0),
则直线FN的斜率为kFN=
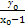,直线ON的斜率为kON=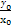.∵FN⊥OM,∴直线OM的斜率为kOM=-
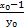.∴直线OM的方程为y=-
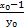x,点M的坐标为M(2,-
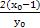).∴直线MN的斜率为kMN=
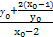.∵MN⊥ON,∴kMNkON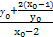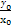=-1.
∴
·=-1.∴
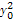+2(x0-1)+x0(x0-2)=0,即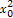+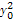=2.∴ON=
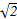为定值.
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
+
=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为
.
=
+
,证明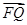
为定值,并求出该值.
：
的离心率
，顶点
的距离为
,
为坐标原点.
两点.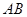
的距离是否为定值.若是请求出这个定值，若不是请说明理由；
的最小值.
右焦点且斜率为1的直线被椭圆截得的弦MN的长为（ ）
,+∞)
,+∞)
,+∞)
+y2=1交于不同两点A,B,则|AB|的最大值为( )
+
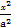=1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .
,且它的长轴长等于圆C:x2+y2-2x-15=0的半径,则椭圆的标准方程是( )
+
=1
+
=1
=1
＝1上一点M作圆x2＋y2＝2的两条切线，点A，B为切点．过A，B的直线l与x轴、y轴分别交于P，Q两点，则△POQ的面积的最小值为( )
