题目内容
如图,已知抛物线C1:x2+by=b2经过椭圆C2: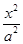 +
+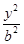 =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.
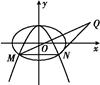
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
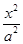 +
+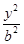 =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
(1) (2)x2+y=1
(2)x2+y=1 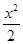 +y2=1
+y2=1
 (2)x2+y=1
(2)x2+y=1 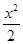 +y2=1
+y2=1解:(1)因为抛物线C1经过椭圆C2的两个焦点F1(-c,0),F2(c,0),
所以c2+b×0=b2,
即c2=b2.
又a2=b2+c2=2c2,
所以椭圆C2的离心率e=
 .
.(2)由(1)可知a2=2b2,
椭圆C2的方程为
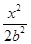 +
+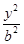 =1.
=1.联立抛物线C1的方程x2+by=b2,
得2y2-by-b2=0,
解得y=-
 或y=b(舍去),
或y=b(舍去),所以x=±
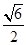 b,
b,即M(
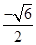 b,-
b,- ),N(
),N(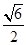 b,-
b,- ),
),所以△QMN的重心坐标为(1,0).
因为重心在C1上,
所以12+b×0=b2,得b=1.
所以a2=2.
所以抛物线C1的方程为x2+y=1,
椭圆C2的方程为
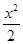 +y2=1.
+y2=1.
练习册系列答案
相关题目
 ,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=
,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ= .
.
 +
+ =1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为
=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为 .
. =
= +
+ ,证明
,证明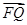 为定值,并求出该值.
为定值,并求出该值. =1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且
=1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且 +5
+5 =0.
=0.
 ,
, 是椭圆长轴的一个端点,
是椭圆长轴的一个端点, 是椭圆短轴的一个端点,
是椭圆短轴的一个端点, 为椭圆的一个焦点.若
为椭圆的一个焦点.若 ,则该椭圆的离心率为 ( )
,则该椭圆的离心率为 ( )






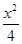 +y2=1的左焦点为F,P为椭圆上一点,其横坐标为
+y2=1的左焦点为F,P为椭圆上一点,其横坐标为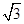 ,则|PF|等于( )
,则|PF|等于( )


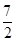
 =3,则C的方程为( )
=3,则C的方程为( ) +y2=1 (B)
+y2=1 (B)  +
+ =1
=1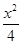 +
+ =1 (D)
=1 (D) 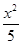 +
+ =1
=1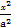 +
+ =1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .
=1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .