题目内容
如果方程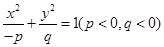
表示双曲线，那么下列椭圆中，与这个双曲线共焦点的是（ ）
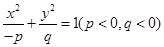表示双曲线，那么下列椭圆中，与这个双曲线共焦点的是（ ）A． | B． |
C． | D． |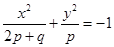
D
试题分析：由方程
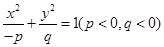表示双曲线，可得c=
，判断出A，C不表示椭圆，再求出B，D中的c，即可得出结论．
练习册系列答案
相关题目
试题分析：由方程
表示双曲线，可得c=，判断出A，C不表示椭圆，再求出B，D中的c，即可得出结论．题目内容
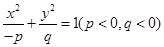表示双曲线，那么下列椭圆中，与这个双曲线共焦点的是（ ）| A． | B． |
| C． | D． |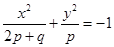
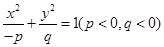表示双曲线，可得c=，判断出A，C不表示椭圆，再求出B，D中的c，即可得出结论．
，且它的四条边与坐标轴平行，正方形GHPQ的顶点G,H在椭圆上，顶点P，Q在正方形的边EF上．且CD=2PQ=
．
)且斜率为k的直线l与椭圆
＋y2＝1有两个不同的交点P和Q.
＋
与
共线？如果存在，求k的值；如果不存在，请说明理由．
+y2=1的左焦点为F,P为椭圆上一点,其横坐标为
,则|PF|等于( )
=3,则C的方程为( )
+y2=1 (B) 
+
=1
+
=1 (D) 
+
=1
右焦点且斜率为1的直线被椭圆截得的弦MN的长为（ ）
右支上的一点，M,N分别是圆(x＋5)2＋y2＝4和(x－5)2＋y2＝1上的点，则|PM|－|PN|的最大值为（ ）
,+∞)
,+∞)
,+∞)
+
=1(a>b>0)的左、右焦点,以原点O为圆心,OF1为半径的圆与椭圆在y轴左侧交于A,B两点,若△F2AB是等边三角形,则椭圆的离心率等于 .