题目内容
(本小题满分13分)已知向量a = 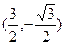 ,b =
,b =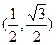 , 且存在实数
, 且存在实数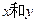 ,使向量m = a
,使向量m = a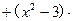 b, n =
b, n = 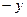 a
a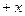 b, 且m⊥n. (Ⅰ)求函数
b, 且m⊥n. (Ⅰ)求函数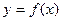 的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意
的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意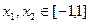 ,都有
,都有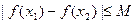 成立?若存在求出M;若不存在,说明理由.
成立?若存在求出M;若不存在,说明理由.
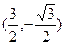 ,b =
,b =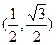 , 且存在实数
, 且存在实数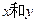 ,使向量m = a
,使向量m = a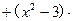 b, n =
b, n = 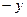 a
a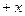 b, 且m⊥n. (Ⅰ)求函数
b, 且m⊥n. (Ⅰ)求函数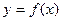 的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意
的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意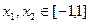 ,都有
,都有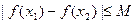 成立?若存在求出M;若不存在,说明理由.
成立?若存在求出M;若不存在,说明理由.(Ⅰ)增区间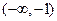 和
和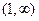
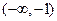 减区间
减区间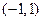 (Ⅱ) M
(Ⅱ) M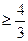
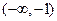 和
和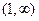
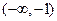 减区间
减区间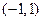 (Ⅱ) M
(Ⅱ) M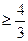
(Ⅰ)a·b= 0,m⊥n,m·n =[a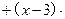 b]·(
b]·( 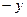 a
a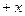 b)
b)
=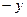 a2
a2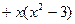 b2 =
b2 =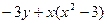 = 0,
= 0,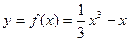 .…………3分
.…………3分
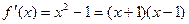 ,在
,在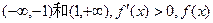 为增函数,
为增函数,
在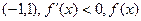 为减函数.……… 5分
为减函数.……… 5分
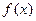 的极大值为
的极大值为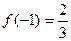 ,
,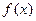 的极小值为
的极小值为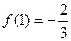 .……… 7分
.……… 7分
(Ⅱ)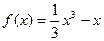 在[1,1]上为减函数,
在[1,1]上为减函数,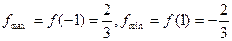 ,
,
对任意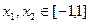 ,都有
,都有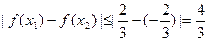 ,故存在正数M
,故存在正数M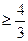 符合要求.
符合要求.
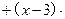 b]·(
b]·( 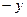 a
a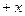 b)
b)=
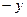 a2
a2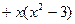 b2 =
b2 =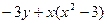 = 0,
= 0,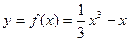 .…………3分
.…………3分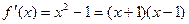 ,在
,在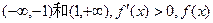 为增函数,
为增函数,在
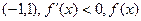 为减函数.……… 5分
为减函数.……… 5分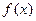 的极大值为
的极大值为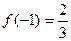 ,
,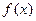 的极小值为
的极小值为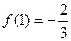 .……… 7分
.……… 7分(Ⅱ)
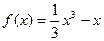 在[1,1]上为减函数,
在[1,1]上为减函数,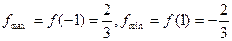 ,
,对任意
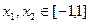 ,都有
,都有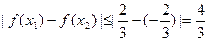 ,故存在正数M
,故存在正数M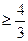 符合要求.
符合要求.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
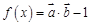 ,其中向量
,其中向量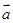 =(
=(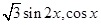 ),
),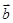 =(1,
=(1,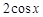 )(
)(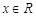 )(1)求
)(1)求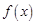 的最小正周期;(2)在△ABC中,角A、B、C的对边分别为
的最小正周期;(2)在△ABC中,角A、B、C的对边分别为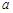 、
、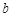 、
、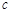 ,
,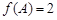 ,
,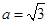 ,
,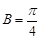 ,求边长b的值.
,求边长b的值. ,则
,则
 ,则
,则
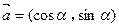 ,
,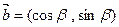
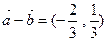 ,
,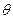 为
为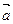 与
与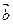 的夹角,求
的夹角,求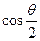 。
。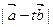 的值最小?
的值最小?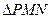 中,
中,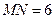 ,则
,则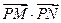 的取值范围是( )
的取值范围是( )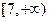
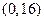
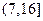

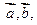 |
|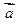 |=3,|
|=3,|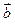 |=2,<
|=2,<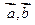 >=600,如果
>=600,如果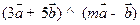 则m的值等于( )
则m的值等于( )
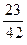
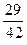
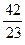
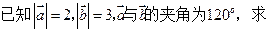
 ;
;
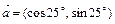 ,
,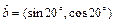 ,若t是实数,且
,若t是实数,且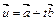 ,则
,则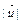 的最小值为
的最小值为