题目内容
在△ABC中,已知向量
=(cos18°,cos72°),
=(2cos63°,2cos27°),则∠BAC=( )
| AB |
| AC |
| A.450 | B.1350 | C.810 | D.990 |
∵
•
=cos18°•2cos63°+cos72°•2cos27°
=2(cos18°sin27°+sin18°cos27°)
=2sin(18°+27°)=2sin45°=
,
|
|=
=
=1,
|
|=
=
=2,
故cos∠BAC=
=
,又0°≤∠BAC≤180°,
所以∠BAC=45°
故选A
| AB |
| AC |
=2(cos18°sin27°+sin18°cos27°)
=2sin(18°+27°)=2sin45°=
| 2 |
|
| AB |
| cos218°+cos272° |
| cos218°+sin218° |
|
| AC |
| 4cos263°+4cos227° |
| 4(sin227°+cos227°) |
故cos∠BAC=
| ||||
|
|
| ||
| 2 |
所以∠BAC=45°
故选A

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
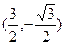 ,b =
,b =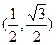 , 且存在实数
, 且存在实数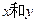 ,使向量m = a
,使向量m = a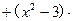 b, n =
b, n = 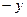 a
a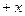 b, 且m⊥n. (Ⅰ)求函数
b, 且m⊥n. (Ⅰ)求函数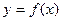 的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意
的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意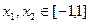 ,都有
,都有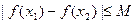 成立?若存在求出M;若不存在,说明理由.
成立?若存在求出M;若不存在,说明理由.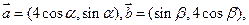
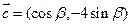 (1)若
(1)若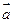 与
与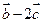 垂直,求
垂直,求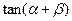 的值;(2)求
的值;(2)求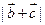 的最大值;
的最大值;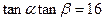 ,求证:
,求证: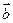 .
.