题目内容
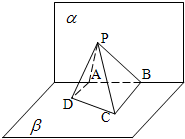
已知三角形PAD所在平面与矩形ABCD所在平面互相垂直，PA=PD=AB=2，∠APD=90°，若点P、A、B、C、D都在同一球面上，则此球的表面积等于（ ）
A．4
| B．
| C．12π | D．20π |
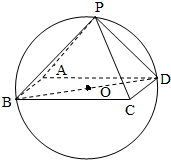
设球心为O，如图．
由PA=PD=AB=2，∠APD=90°，可求得AD=2
，
在矩形ABCD中，可求得对角线BD=
=2
，
由于点P、A、B、C、D都在同一球面上，
∴球的半径R=
BD=
则此球的表面积等于=4πR2=12π．
故选：C．
由PA=PD=AB=2，∠APD=90°，可求得AD=2
| 2 |
在矩形ABCD中，可求得对角线BD=
22+(2
|
| 3 |
由于点P、A、B、C、D都在同一球面上，
∴球的半径R=
| 1 |
| 2 |
| 3 |
则此球的表面积等于=4πR2=12π．
故选：C．
练习册系列答案
轻松暑假总复习系列答案
相关题目
