题目内容
17．已知复数z=$\frac{2}{-1+i}$，则下列判断正确的是（ ）| A． | z的实部为1 | B． | |z|=$\sqrt{2}$ | ||
| C． | z的虚部为-i | D． | z的共轭复数为1+i |
分析 通过化简复数z即得结论．
解答 解：z=$\frac{2}{-1+i}$=$\frac{2（-1-i）}{（-1+i）（-1-i）}$=$\frac{-2-2i}{1-{i}^{2}}$=-1-i，
∴|z|=$\sqrt{（-1）^{2}+（-1）^{2}}$=$\sqrt{2}$，
故选：B．
点评 本题考查复数的相关知识，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
7．若一个几何体的正视图，侧视图和俯视图形状相同，大小均相等，那么这个几何体不可以是（ ）
| A． | 球 | B． | 三棱锥 | C． | 正方体 | D． | 圆柱 |
8．已知集合A=[-4，1），B={0，2}，则A∩B为（ ）
| A． | {0} | B． | {2} | C． | {0，3} | D． | {x|-4＜x＜1} |
2．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两条渐近线都与圆（x-c）2+y2=ac（c=$\sqrt{{a}^{2}+{b}^{2}}$相切，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | 2 | D． | $\frac{1+\sqrt{5}}{2}$ |
6．某几何体的三视图如图所示，则该几何体的体积为（ ）
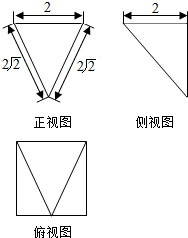
| A． | $\frac{4\sqrt{6}}{3}$ | B． | 2$\sqrt{6}$ | C． | $\frac{4\sqrt{7}}{3}$ | D． | 4$\sqrt{7}$ |
在以棱长为1的正方形ABCD-A1B1C1D1中，求：