题目内容
12.已知PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=1,则AC=2$\sqrt{3}$.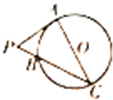
分析 连接AB,根据弦切角定理及三角形相似的判定,我们易得△PBA~△ABC,再由相似三角形的性质,我们可以建立未知量与已知量之间的关系式,解方程即可求解.
解答 解:依题意,我们知道△PBA~△ABC,
由相似三角形的对应边成比例性质我们有$\frac{PA}{2R}=\frac{PB}{AB}$,
即2R=$\frac{PA•AB}{PB}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 在平面几何中,我们要求线段的长度,关键是寻找未知量与已知量之间的关系,寻找相似三角形和全等三角形是常用的方法,根据相似三角形的性质,很容易得到已知量与未知量之间的关系,解方程即可求解.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
2.从某5人中选派3人分别参加数学、物理、化学竞赛,每个学科各1人,其中甲、乙两人至多选1人参赛,则不同的参赛方案共有( )
| A. | 24种 | B. | 36种 | C. | 42种 | D. | 48种 |
17.已知复数z=$\frac{2}{-1+i}$,则下列判断正确的是( )
| A. | z的实部为1 | B. | |z|=$\sqrt{2}$ | ||
| C. | z的虚部为-i | D. | z的共轭复数为1+i |
