题目内容
6.某几何体的三视图如图所示,则该几何体的体积为( )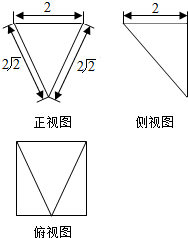
| A. | $\frac{4\sqrt{6}}{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{4\sqrt{7}}{3}$ | D. | 4$\sqrt{7}$ |
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的四棱锥,求出底面面积,代入棱锥体积公式,可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的四棱锥,
其底面面积S=2×2=4,
高h=$\sqrt{(2\sqrt{2})^{2}-(\frac{2}{2})^{2}}$=$\sqrt{7}$,
故棱锥的体积V=$\frac{1}{3}Sh$=$\frac{4\sqrt{7}}{3}$,
故选:C.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
16.如图所示,某三棱锥的正视图、俯视图均为边长为2的正三角形,则其左视图面积为( )
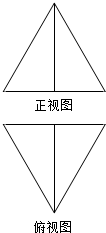

| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
17.已知复数z=$\frac{2}{-1+i}$,则下列判断正确的是( )
| A. | z的实部为1 | B. | |z|=$\sqrt{2}$ | ||
| C. | z的虚部为-i | D. | z的共轭复数为1+i |
18.△ABC的内角A,B,C的对边分别为a,b,c,已知a=2,b=2$\sqrt{3}$,A=$\frac{π}{6}$,则△ABC的面积为( )
| A. | $2\sqrt{3}$或$\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{3}$或$4\sqrt{3}$ | D. | $\sqrt{3}$ |