题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}{-{e}^{2x}+bx+c,}&{x≤1}\\{a({x}^{2}lnx-x+1)+1,}&{x≥1}\end{array}\right.$(Ⅰ)若0<b<2e2,试讨论函数f(x)在区间(-∞,1]上的单调性;
(Ⅱ)若函数f(x)在x=0处取得极值1,求f(x)在区间[-2,2]上的最大值.
分析 (Ⅰ)当x≤1时,f′(x)=-2e2x+b,令f′(x)=0得导函数有唯一零点x=$\frac{1}{2}ln\frac{b}{2}$,讨论各区间上导函数的符号,可得函数f(x)在区间(-∞,1]上的单调性;
(Ⅱ)根据函数f(x)在x=0处取得极值1,可求出b,c的值,对a进行分类讨论,可得a取不同值时,f(x)在区间[-2,2]上的最大值.
解答 解:(Ⅰ)当x≤1时,f′(x)=-2e2x+b,
易知函数f′(x)为(-∞,1]上的减函数,令f′(x)=0得导函数有唯一零点x=$\frac{1}{2}ln\frac{b}{2}$,
因为0<b<2e2,因此x=$\frac{1}{2}ln\frac{b}{2}$<1,故导数值在(-∞,$\frac{1}{2}ln\frac{b}{2}$)为正,在($\frac{1}{2}ln\frac{b}{2}$,1]为负,
所以函数f(x)在(-∞,$\frac{1}{2}ln\frac{b}{2}$)为增函数,在($\frac{1}{2}ln\frac{b}{2}$,1]为减函数;
(Ⅱ)由题意当x=0时,f(0)=c-1=1,
∴c=2,
当x<1时,f′(x)=-2e2x+b,
依题意得f′(0)=b-2=0,
∴b=2,
经检验b=2,c=2符合条件,因此f(x)=$\left\{\begin{array}{l}-{e}^{2x}+2x+2,&x≤1\\ a({x}^{2}lnx-x+1)+1,&x≥1\end{array}\right.$
当-2≤x≤1时,f(x)=-e2x+2x+2,f′(x)=-2e2x+2,
令f′(x)=0得x=0当x变化时,f′(x),f(x)的变化情况如下表:
| x | -2 | (-2,0) | 0 | (0,1) | 1 |
| f′(x) | + | 0 | - | ||
| f(x) | -e-4-2 | 递增 | 极大值1 | 递减 | 4-e2 |
当1<x≤2时,f(x)=a(x2lnx-x+1)+1.
f′(x)=a(2xlnx+x-1),
令g(x)=2xlnx+x-1,
当1<x≤2时,显然g(x)>0恒成立,
当a<0时,f′(x)=a(2xlnx+x-1)<0,
f(x)在(1,2]单调递减,所以f(x)<f(1)=1恒成立.
此时函数在[-2,2]上的最大值为1;
当a=0时,在(1,2]上f(x)=1,
当a>0时,在(1,2]上f′(x)=a(2xlnx+x-1)>0
所以在(1,2]上,函数f(x)为单调递增函数.
∴f(x)在(1,2]最大值为a(4ln2-1)+1,
∵a(4ln2-1)+1>1,故函数f(x)在[-2,2]上最大值为a(4ln2-1)+1.
综上:当a≤0时,f(x)在[-2,2]上的最大值为1;
当a>0时,f(x)在[-2,2]最大值为a(4ln2-1)+1.
点评 本题考查的知识点是分段函数的应用,导数法确定函数的单调性和最值,是分段函数与导数的综合应用,难度较大,属于难题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案| A. | z的实部为1 | B. | |z|=$\sqrt{2}$ | ||
| C. | z的虚部为-i | D. | z的共轭复数为1+i |
| A. | $2\sqrt{3}$或$\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{3}$或$4\sqrt{3}$ | D. | $\sqrt{3}$ |
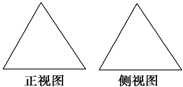 如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )