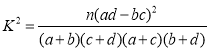题目内容
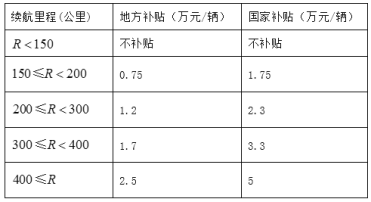
【题目】为节能环保,推进新能源汽车推广和应用,对购买纯电动汽车的用户进行财政补贴. 某地补贴政策如下(![]() 表示纯电续航里程):
表示纯电续航里程):
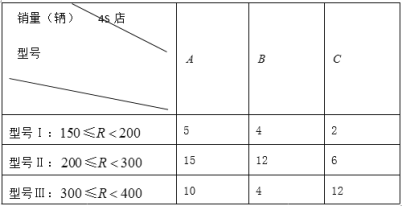
有![]() 三个纯电动汽车4s店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下: (每位客户只能购买一辆纯电动汽车)
三个纯电动汽车4s店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下: (每位客户只能购买一辆纯电动汽车)

(Ⅰ)从上述购买纯电动汽车的客户中随机选一人,求此人购买的是![]() 店纯电动汽车且享受补贴不低于3.5万元的概率;
店纯电动汽车且享受补贴不低于3.5万元的概率;
(Ⅱ)从购买![]() 店纯电动汽车的客户中按分层抽样的方法随机选6人,再从这6人中随机选2人,进行使用满意度的调查,求这两人享受补贴恰好相同的概率;
店纯电动汽车的客户中按分层抽样的方法随机选6人,再从这6人中随机选2人,进行使用满意度的调查,求这两人享受补贴恰好相同的概率;
(Ⅲ)分别用![]() 表示购买
表示购买![]() 店和
店和![]() 店纯电动汽车客户享受补贴的平均值,比较
店纯电动汽车客户享受补贴的平均值,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)由题意可知,购买纯电动汽车的客户共70人,此人购买的是![]() 店纯电动汽车且享受补贴不低于3.5万元的结果共16个,由此能求出结果;(Ⅱ)按分层抽样的方法任选6人,购买三种型号纯电动汽车的人数分别为1,3,2,用列法列出基本事件总数,这两人享受补贴恰好相同包含的基本事件个数为4,由此能结果;(Ⅲ)结合表格可知
店纯电动汽车且享受补贴不低于3.5万元的结果共16个,由此能求出结果;(Ⅱ)按分层抽样的方法任选6人,购买三种型号纯电动汽车的人数分别为1,3,2,用列法列出基本事件总数,这两人享受补贴恰好相同包含的基本事件个数为4,由此能结果;(Ⅲ)结合表格可知![]() .
.
(Ⅰ)由题意可知,从![]() 三个纯电动汽车
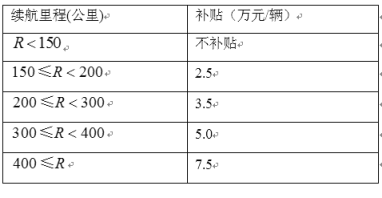
三个纯电动汽车![]() 店购买纯电动汽车的客户共70人,购买型号Ⅰ,型号Ⅱ,型号Ⅲ纯电动汽车享受补贴分别为2.5万元,3.5万元,5万元.
店购买纯电动汽车的客户共70人,购买型号Ⅰ,型号Ⅱ,型号Ⅲ纯电动汽车享受补贴分别为2.5万元,3.5万元,5万元.
从上述购买纯电动汽车的客户中任选一人共70个等可能的结果,此人购买的是![]() 店纯电动汽车且享受补贴不低于3.5万元(购买型号Ⅱ或型号Ⅲ)的结果共16个
店纯电动汽车且享受补贴不低于3.5万元(购买型号Ⅱ或型号Ⅲ)的结果共16个
所以所求概率为![]() .
.
(Ⅱ)![]() 店客户中购买Ⅰ,型号Ⅱ,型号Ⅲ纯电动汽车的人数为
店客户中购买Ⅰ,型号Ⅱ,型号Ⅲ纯电动汽车的人数为![]() ,按分层抽样的方法任选6人,则6人中购买型号Ⅰ,型号Ⅱ,型号Ⅲ纯电动汽车的人数为
,按分层抽样的方法任选6人,则6人中购买型号Ⅰ,型号Ⅱ,型号Ⅲ纯电动汽车的人数为![]() ,记做
,记做![]() .从这6人中任选2人的结果为
.从这6人中任选2人的结果为
![]() 共15种,其中两人享受补贴恰好相同(即购买同型号汽车)的结果为
共15种,其中两人享受补贴恰好相同(即购买同型号汽车)的结果为![]() 共4种,所以所求概率为
共4种,所以所求概率为![]() .
.
(Ⅲ)![]()

 阅读快车系列答案
阅读快车系列答案【题目】在甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下的2×2列联表.已知在全部105人中抽到随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可能性要求,能否认为“成绩与班级有关系”?
P(K2≥x0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式及数据:K2=![]() .
.
【题目】某高校共有学生15000人,其中男生10500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).
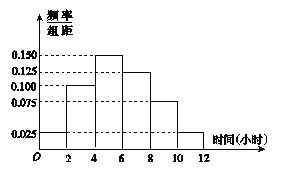
(1)应收集多少位女生的样本数据?
(2)根据这200个样本数据,得到学生每周平均体育运动时间的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .估计该校学生每周平均体育运动时间超过4小时的概率.
.估计该校学生每周平均体育运动时间超过4小时的概率.
(3)在样本数据中,有40位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.(把表简要画在答题卡上)
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |