Question

【题目】已知椭圆：过点，且一个焦点坐标为．

（Ⅰ）求椭圆的方程及离心率；

（Ⅱ）过点且与x轴不垂直的直线与椭圆C交于两点，若在线段上存在点，使得以MP, MQ为邻边的平行四边形是菱形，求m的取值范围.

Answer 1

【答案】（Ⅰ），（Ⅱ）

【解析】

（Ⅰ）由题意可得，，根据，即可求出，再椭圆方程可求，即可求出离心率；（Ⅱ）把直线方程与椭圆的方程联立求出与、两点的坐标有关的等量关系，进而求出的中点坐标，再利用菱形的对角线互相垂直即可求出的取值范围．

（Ⅰ）由椭圆过点，一个焦点坐标为，可知

所以

所以椭圆的方程为.

离心率

（Ⅱ）设， ，

代入椭圆，得：

，所以，

所以中点的坐标为

因为以为邻边的平行四边形是菱形，所以

所以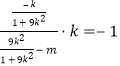，即

因为，所以.

又点在线段上，所以.

综上，