题目内容
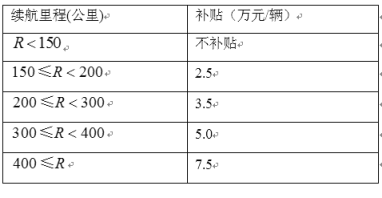
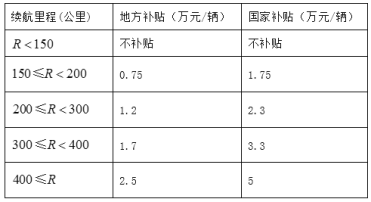
【题目】为节能环保，推进新能源汽车推广和应用，对购买纯电动汽车的用户进行财政补贴，财政补贴由地方财政补贴和国家财政补贴两部分组成. 某地补贴政策如下（
表示纯电续航里程）：
有
三个纯电动汽车
店分别销售不同品牌的纯电动汽车，在一个月内它们的销售情况如下：
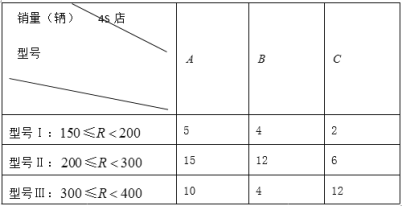
（每位客户只能购买一辆纯电动汽车）
（1）从上述购买纯电动汽车的客户中随机选一人，求此人购买的是
店纯电动汽车且享受补贴不低于3.5万元的概率；
（2）从上述
两个纯电动汽车店的客户中各随机选一人，求恰有一人享受5万元财政补贴的概率；
（3）从上述三个纯电动汽车店的客户中各随机选一人， 这3个人享受的财政补贴分别记为
. 求随机变量
的分布列. 试比较数学期望
的大小；比较方差
的大小. （只需写出结论）
【答案】（1）
；（2）
；（3）
，
.
【解析】
（1）由题意知从A，B，C三个纯电动汽车4s店购买纯电动汽车的客户共70人，购买型号Ⅰ，型号Ⅱ，型号Ⅲ纯电动汽车享受补贴分别为2.5万元，3.5万元，5万元，从上述购买纯电动汽车的客户中任选一人，共70个结果，此人购买的是B店纯电动汽车且享受补贴不低于3.5万元（购买型号Ⅱ或型号Ⅲ）的结果共16个，由此能求出此人购买的是B店纯电动汽车且享受补贴不低于3.5万元的概率．
（2）从上述B，C纯电动汽车4s店的客户中各随机抽取一人，共400个等可能结果，其中恰有一人享受5万元财政补贴（即1人购买型号Ⅲ，1人没有购买型号Ⅲ）的结果为4×8+16×12＝224，由此能求出恰有一人享受5万元财政补贴的概率．
（3）随机变量XA的可能取值为2.5，3.5，5，分别求出相应的概率，由此能求出随机变量XA的分布列，由题意E（XC）＞E（XA）＞E（XB），D（XC）＞D（XA）＞D（XB）．
（1）由题意可知，从
三个纯电动汽车
店购买纯电动汽车的客户共70人，购买型号Ⅰ，型号Ⅱ，型号Ⅲ纯电动汽车享受补贴分别为2.5万元，3.5万元，5万元.
从上述购买纯电动汽车的客户中任选一人共70个等可能的结果，
此人购买的是
店纯电动汽车且享受补贴不低于3.5万元（购买型号Ⅱ或型号Ⅲ）的结果共16个,
所以所求概率为
.
（2）从上述
纯电动汽车店的客户中各随机选一人共
个等可能的结果.其中恰有一人享受5万元财政补贴（即1人购买型号Ⅲ，1人没购买型号Ⅲ）的结果为
，所求概率为
.
（3）随机变量
的分布列为
| 2.5 | 3.5 | 5 |
|
|
|
|
，.
