题目内容
(本小题满分14分)
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求f(x)的解析式;
(2)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(3)若当x=1时,函数y=g(x)取得极值,确定y=g(x)的单调区间.
已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求f(x)的解析式;
(2)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(3)若当x=1时,函数y=g(x)取得极值,确定y=g(x)的单调区间.
解:(1)∵f(x)为偶函数,∴b=0. …………………2分
又f(x)过(2,5),∴4+c=5,得c=1.
∴f(x)= x2+1 …………………4分
(2)又g(x) =(x+a)f(x)=(x+a)(x2+1)=x3+ax2+x+a
=(x+a)f(x)=(x+a)(x2+1)=x3+ax2+x+a
由题意得g′(x)=3x2+2ax+1=0有解,
∴Δ=4a2-12>0,得a>或a<-. …………………9分
(3)由(1)知g′(x)=3x2+2ax+1,由题意得g′(1)=0,得a=-2,经检验当a=-2时,y=g(x)取得极值符合题意,由g′(x)=3x2-4x+1>0,得x>1或x<,由g′(x)<0,得<x<1,
故g(x)的单调增区间为,(1,+∞),单调减区间为 . …………………14分
. …………………14分
又f(x)过(2,5),∴4+c=5,得c=1.
∴f(x)= x2+1 …………………4分
(2)又g(x)
 =(x+a)f(x)=(x+a)(x2+1)=x3+ax2+x+a
=(x+a)f(x)=(x+a)(x2+1)=x3+ax2+x+a由题意得g′(x)=3x2+2ax+1=0有解,
∴Δ=4a2-12>0,得a>或a<-. …………………9分
(3)由(1)知g′(x)=3x2+2ax+1,由题意得g′(1)=0,得a=-2,经检验当a=-2时,y=g(x)取得极值符合题意,由g′(x)=3x2-4x+1>0,得x>1或x<,由g′(x)<0,得<x<1,
故g(x)的单调增区间为,(1,+∞),单调减区间为
 . …………………14分
. …………………14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
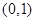 且与曲线
且与曲线 在点
在点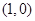 处切线垂直的直线方程是( )
处切线垂直的直线方程是( )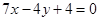
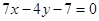
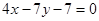

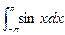 的值为( )
的值为( )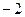
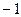
 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为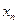 ,则
,则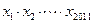 的值为( )
的值为( ) 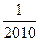
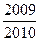
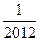
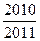

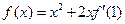 ,若
,若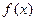 在R上可导,则
在R上可导,则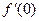 = ,
= ,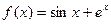 ,则
,则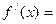
 ;
;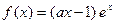 (
(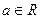 )在区间
)在区间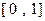 上是单调增函数,则实数
上是单调增函数,则实数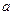 的取值范围是
的取值范围是 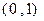
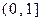
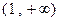
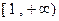
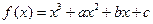 在
在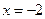 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线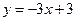 在点( 1 , 0
在点( 1 , 0 ) 处相
) 处相 切, 求a , b , c的值。
切, 求a , b , c的值。