题目内容
15.设函数f(x)=|x+$\frac{1}{a}$|+|x-a|(a>0)(1)证明:f(x)≥2;
(2)若f(2)<3,求实数a的取值范围.
分析 (1)由条件利用绝对值三角不等式求得f(x)≥|a|+|$\frac{1}{a}$|,再利用基本不等式证得|a|+|$\frac{1}{a}$|≥2,从而证得结论.
(2)f(2)<3,即|2+$\frac{1}{a}$|+|2-a|<3,再分类讨论求得a的范围,综合可得结论.
解答 解:(1)证明:∵f(x)=|x+$\frac{1}{a}$|+|x-a|≥|(x+$\frac{1}{a}$)-(x-a)|=|a+$\frac{1}{a}$|=|a|+|$\frac{1}{a}$|≥2,
故f(x)≥2 成立.
(2)f(2)<3,即|2+$\frac{1}{a}$|+|2-a|<3,
当a>1 时,可得2+$\frac{1}{a}$+|a-2|<3,即|a-2|<1-$\frac{1}{a}$,即$\frac{1}{a}$-1<a-2<1-$\frac{1}{a}$,可得$\left\{\begin{array}{l}{a>1}\\{a-\frac{1}{a}>1}\\{a+\frac{1}{a}<3}\end{array}\right.$,
求得 $\frac{1+\sqrt{5}}{2}$<a<$\frac{3+\sqrt{5}}{2}$.
a=1 时,可得|2+1|+|2-1|<3不成立,故a≠1.
0<a<1时,可得 2+$\frac{1}{a}$+2-a<3,即 a-$\frac{1}{a}$>1,即 $\left\{\begin{array}{l}{0<a<1}\\{a-\frac{1}{a}>1}\end{array}\right.$,求得a∈∅.
综上可得,$\frac{1+\sqrt{5}}{2}$<a<$\frac{3+\sqrt{5}}{2}$.
点评 本题主要考查绝对值三角不等式,绝对值不等式的解法,基本不等式的应用,体现了转化、分类讨论的数学思想,属于中档题.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | $\frac{5}{4}$或-$\frac{5}{4}$ | B. | $\frac{5}{2}$或-$\frac{5}{2}$ | C. | $\frac{5}{8}$或-$\frac{5}{8}$ | D. | $\frac{5}{16}$或-$\frac{5}{16}$ |
| 零件数 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)推出是正相关还是负相关;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
| A. | 当a>0时有最大值 | B. | 当a>1时有最小值 | ||
| C. | 当a<0时有最大值 | D. | 当0<a<1时有最小值 |
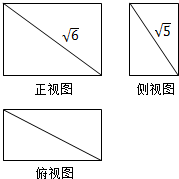 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的长度为$\sqrt{6}$,在侧视图中的长度为$\sqrt{5}$,则该长方体的表面积为3+4$\sqrt{11}$.