题目内容
【题目】已知数列{an}的各项均为正数,其前n项和为Sn , 且满足a1=1,an+1=2 ![]() +1,n∈N* .
+1,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)是否存在正整数k,使ak , S2k﹣1 , a4k成等比数列?若存在,求k的值,若不存在,请说明理由.
【答案】
(1)解:因为a1=1,an+1=2 ![]() +1,
+1,
所以a2=2 ![]() +1=2+1=3
+1=2+1=3
(2)解:由an+1=2 ![]() +1得,
+1得, ![]() ,
,
所以当n≥2时, ![]() ,
,
两个式子相减得,4an=(an+1+an﹣2)(an+1﹣an),
化简得,(an+1﹣an﹣2)(an+1+an)=0,
因为数列{an}的各项均为正数,
所以an+1﹣an﹣2=0,即an+1﹣an=2,
所以数列{an}是以1为首项、2为公差的等差数列,
则an=1+(n﹣1)×2=2n﹣1
(3)解:假设存在正整数k使ak,S2k﹣1,a4k成等比数列,
则 ![]() ,
,
所以 ![]() =(2k﹣1)(8k﹣1),
=(2k﹣1)(8k﹣1),
(2k﹣1)3=8k﹣1,化简得4k2﹣6k﹣1=0,
解得 ![]() ,
, ![]() ,
,
因为k是正整数,所以不存在正整数k满足条件
【解析】(1)将n=1代入式子即可求解;(2)由an+1=2 ![]() +1得
+1得 ![]() ,令n取n﹣1代入上式可得
,令n取n﹣1代入上式可得 ![]() ,两个式子相减后进行化简,利用等差数列的定义判断,再由等差数列的通项公式求出an;(3)先假设存在正整数k满足条件,利用等比中项的性质、等差数列的前n项和公式、通项公式列出方程,化简后求出k的值,再由k是正整数进行判断.
,两个式子相减后进行化简,利用等差数列的定义判断,再由等差数列的通项公式求出an;(3)先假设存在正整数k满足条件,利用等比中项的性质、等差数列的前n项和公式、通项公式列出方程,化简后求出k的值,再由k是正整数进行判断.
【考点精析】解答此题的关键在于理解等比关系的确定的相关知识,掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为
之间是正相关还是负相关;若该地1月份某天的最低气温为![]() ,请用所求回归方程预测该店当日的销售量;
,请用所求回归方程预测该店当日的销售量;
(3)设该地1月份的日最低气温![]() ~
~![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
, ![]() 近似为样本方差
近似为样本方差![]() ,求
,求![]() .
.
附:①回归方程![]() 中,
中, 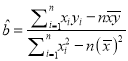 ,
, ![]() .
.
②![]() ,
, ![]() ,若
,若![]() ~
~![]() ,则
,则![]() ,
, ![]() .
.