题目内容
【题目】已知直线![]() 与
与![]() 、
、![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(Ⅰ)若点![]() 、
、![]() 分别是双曲线
分别是双曲线![]() 的虚轴、实轴的一个端点,试在平面上找两点
的虚轴、实轴的一个端点,试在平面上找两点![]() 、
、![]() ,使得双曲线
,使得双曲线![]() 上任意一点到
上任意一点到![]() 、
、![]() 这两点距离差的绝对值是定值.
这两点距离差的绝对值是定值.
(Ⅱ)若以原点![]() 为圆心的圆
为圆心的圆![]() 截直线
截直线![]() 所得弦长是
所得弦长是![]() ,求圆
,求圆![]() 的方程以及这条弦的中点.
的方程以及这条弦的中点.
【答案】(Ⅰ) ![]() ,
, ![]() 或
或![]() ,
, ![]() .(Ⅱ)圆
.(Ⅱ)圆![]() 的方程为
的方程为![]() ,弦
,弦![]() 的中点为
的中点为![]() .
.
【解析】试题分析:
(Ⅰ)由几何关系可知![]() ,
, ![]() 是双曲线的焦点,则
是双曲线的焦点,则![]() ,
, ![]() 或
或![]() ,
, ![]() ;
;
(Ⅱ)利用弦长公式可求得半径为3,求得圆的方程为![]() ,则弦
,则弦![]() 的中点为
的中点为![]() .
.
试题解析:
(Ⅰ)∵直线![]() 与
与![]() 轴,
轴, ![]() 轴交于
轴交于![]() ,
, ![]() 两点,∴
两点,∴![]() ,
, ![]() ,
,
又![]() 、
、![]() 分别是双曲线
分别是双曲线![]() 的虚轴,实轴的一个端点,
的虚轴,实轴的一个端点,
∴双曲线中![]() ,
, ![]() ,
, ![]() ,
,
由题可知![]() ,
, ![]() 是双曲线的焦点,
是双曲线的焦点,
∴![]() ,
, ![]() 或
或![]() ,
, ![]() .
.
(Ⅱ)圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴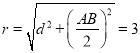 ,
,
∴圆![]() 的方程为
的方程为![]() ,
,
设![]() 的中点为
的中点为![]() 则:
则:
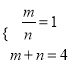 ,解
,解![]() ,
,
即弦![]() 的中点为
的中点为![]() .
.

练习册系列答案
相关题目
