题目内容
【题目】已知函数
， 
．
（1）讨论函数
的单调性；
（2）若
在定义域内恒成立，求实数
的取值范围．
【答案】（1）见解析（2）
或
.
【解析】试题分析：
(1)由题意可得： 
.分类讨论：
①若
时，， 
在
上是增函数.
②若
时，则
在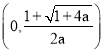
上是增函数.在
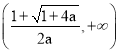上是减函数.
(2)不等式恒成立，则：①当
， 
同时恒成立时，
②当
， 
同时恒成立时，
③当
时，∵
为增函数， 
为减函数,
综上： 
或
.
试题解析：
解：（1）
.
①若
时，
，则
在
上是增函数.
②若
在
上是增函数.
在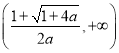
上是减函数.
（2）若
在定义域内恒成立,考虑以下情形:
①当
， 
同时恒成立时，
由
， 
恒成立.
得： 
.
∵由
， 
恒成立得： 
.∴
.
②当
， 
同时恒成立时， 
不存在；
③当
时，∵
为增函数， 
为减函数,
若它们有共同零点，则
恒成立.
由
， 
,联立方程组解得： 
.
综上： 
或
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】如图，矩形
中， 
， 
为边
的中点，将
沿直线
翻转成
.若
为线段
的中点，则在
翻折过程中：
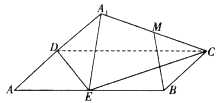
①
是定值；②点
在某个球面上运动；
③存在某个位置，使
；④存在某个位置，使
平面
.
其中正确的命题是_________.
【题目】某同学用“随机模拟方法”计算曲线
与直线
， 
所围成的曲边三角形的面积时，用计算机分别产生了10个在区间
上的均匀随机数
和10个区间
上的均匀随机数
（
， 
），其数据如下表的前两行.
| 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得这个曲边三角形面积的一个近似值是（ ）
A. 
B. 
C. 
D. 
