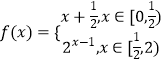题目内容
【题目】已知函数f（x）=x3﹣3x
（1）求函数f（x）的单调区间，并求函数f（x）的极值；
（2）若方程x3﹣3x﹣a+1=0有三个相异的实数根，求a的取值范围．
【答案】
（1）解：f'（x）=3x2﹣3由f'（x）=0解得x=±1
列表如下：
x | （﹣∞，﹣1） | ﹣1 | （﹣1，1） | 1 | （1，+∞） |
f'（x） | + | 0 | ﹣ | 0 | + |
f（x） | ↗ | 极大值f（﹣1） | ↘ | 极小值f（1） | ↗ |
所以函数的单调递增区间是（﹣∞，﹣1），（1，+∞）
单调递减区间是（﹣1，1）
函数的极大值是f（﹣1）=2，极小值是f（1）=﹣2
（2）解：方程x3﹣3x﹣a+1=0即为方程x3﹣3x=a﹣1
令y=x3﹣3x和y=a﹣1，方程x3﹣3x﹣a+1=0有三个相异的实数根即上述两个函数的图象有三个不同的交点y=a﹣1是一条直线而y=x3﹣3x的图象大致如下：
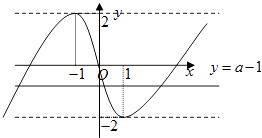
如图要使两个函数的图象有三个不同的交点
则有：﹣2＜a﹣1＜2，解得：﹣1＜a＜3
【解析】（1）先求导数fˊ（x）然后在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0，fˊ（x）＞0的区间为单调增区间，fˊ（x）＜0的区间为单调减区间，从而求函数f（x）的极值；（2）方程x3﹣3x﹣a+1=0即为方程x3﹣3x=a﹣1，令y=x3﹣3x和y=a﹣1，方程x3﹣3x﹣a+1=0有三个相异的实数根，转化为判断两个函数何时有三个不同交点的问题，数形结合，问题得解．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数的极值的方法是:（1）如果在
附近的左侧
,右侧
,那么
是极大值（2）如果在附近的左侧,右侧
,那么
是极小值才能正确解答此题．
名校课堂系列答案
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了50人，他们年龄大点频率分布及支持“生育二胎”人数如下表：
年龄 |
|
|
|
|
|
|
频率 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
（1）由以上统计数据填下面2乘2列联表，并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异：
（2）若对年龄在
的被调查人中随机选取两人进行调查，恰好这两人都支持“生育二胎放开”的概率是多少？
参考数据： 
， 
， 
.
