Question

【题目】已知函数f（x）=xsinx，有下列四个结论： ①函数f（x）的图象关于y轴对称；
②存在常数T＞0，对任意的实数x，恒有f（x+T）=f（x）；
③对于任意给定的正数M，都存在实数x0 ， 使得|f（x0）|≥M；
④函数f（x）在[0，π]上的最大值是 ．
其中正确结论的序号是（请把所有正确结论的序号都填上）．

Answer 1

【答案】①③
【解析】解：对于①，∵f（﹣x）=﹣xsin（﹣x）=xsinx=f（x），∴函数为偶函数，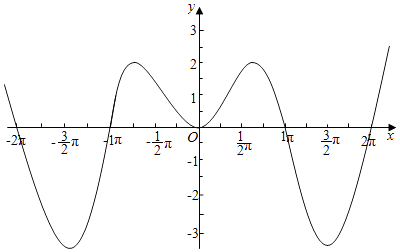
∴函数f（x）的图象关于y轴对称，故①正确；
对于②∵当x=2kπ+ 时，f（x）=x，随着x的增大函数值也在增大，所以不会是周期函数，故②错；
对于③∵|sinx0|≤1，∴对任意给定的正数M，都存在实数x0 ， 使得|f（x0）|≥M，故③正确；对于④，f（ ）= ．∵f′（x）=sinx+xcosx，∴f′（ ）=1，∴ 不是函数的极值点，故④不正确
所以答案是：①③．