题目内容
19.已知函数f(x)=ax-lnx,a∈R.(Ⅰ) 若曲线y=f(x)在点(1,f(1))处切线的斜率为1,求a的值;
(Ⅱ) 讨论函数f(x)极值点的个数;
(Ⅲ) 若f(x)≤xlnx在[1,+∞)上恒成立,求a的取值范围.
分析 (Ⅰ)先求出函数f(x)的导数,根据f′(1)=1,从而求出a的值;
(Ⅱ)先求出函数f(x)的导数,通过讨论a的范围,从而得到函数的极值点的个数;
(Ⅲ)问题转化为$a≤\frac{lnx}{x}+lnx$在[1,+∞)上恒成立,令$g(x)=\frac{lnx}{x}+lnx$,通过求导得到函数g(x)的单调性,从而有g(x)min=g(1)=0,进而求出a的范围.
解答 解:(Ⅰ) 由f(x)=ax-lnx,得$f'(x)=a-\frac{1}{x}$,
又$f'(1)=a-\frac{1}{1}=1$,
∴a=2;
(Ⅱ)∵$f'(x)=a-\frac{1}{x}=\frac{ax-1}{x}$,x>0,
当a≤0时,f′(x)≤0在(0,+∞)上恒成立,
函数f(x)在(0,+∞)上单调递减;
∴f(x)在(0,+∞)上没有极值点,
当a>0时,f′(x)≤0得$0<x≤\frac{1}{a}$,f′(x)≥0得$x≥\frac{1}{a}$,
∴f(x)在$(0,\frac{1}{a}]$上单调递减,在$[\frac{1}{a},+∞)$上单调递增,
∴f(x)在$x=\frac{1}{a}$有极小值.
综上得 当a≤0时,f(x)在(0,+∞)上没有极值点;
当a>0时,f(x)在(0,+∞)上有一个极值点.
(Ⅲ) f(x)<xlnx在[1,+∞)上恒成立,
即$a≤\frac{lnx}{x}+lnx$在[1,+∞)上恒成立,
令$g(x)=\frac{lnx}{x}+lnx$,x∈[1,+∞),
∴$g'(x)=\frac{1-lnx}{x^2}+\frac{1}{x}=\frac{x-lnx+1}{x^2}$,
令h(x)=x-lnx+1,
∴$h'(x)=1-\frac{1}{x}=\frac{x-1}{x}≥0$在[1,+∞)上恒成立,
∴h(x)在[1,+∞)上单调递增,
∴h(x)≥h(1)=2,
∴g'(x)>0在[1,+∞)上恒成立,
∴g(x)在[1,+∞)上单调递增,
∴g(x)min=g(1)=0,
∴a≤0.
点评 本题考查了函数的单调性,函数的极值问题,考查导数的应用,考查转化思想,本题属于难题.

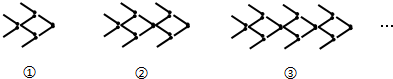
按照上面的规律,第10个“金鱼”图需要火柴棒的根数为( )
| A. | 58 | B. | 78 | C. | 62 | D. | 82 |
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -1 |
| A. | 5 | B. | 2 | C. | -7 | D. | 14 |