Question

【题目】如图，在Rt△ABC中，∠ACB＝，AC＝3， BC＝2，P是△ABC内的一点．

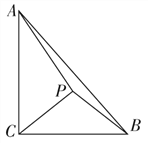
（1）若P是等腰直角三角形PBC的直角顶点，求PA的长；

（2）若∠BPC＝，设∠PCB＝θ，求△PBC的面积S(θ)的解析式，并求S(θ)的最大值．

Answer 1

【答案】(1) （2）S(θ)＝ ，S(θ)的最大值为

【解析】试题分析：（1）在△PAC中，已知两边一角求第三边，根据余弦定理可得（2）先由正弦定理用θ表示PC，再根据三角形面积公式得S(θ)，利用二倍角公式以及配角公式将S(θ)化为基本三角函数形式，再根据正弦函数性质求最大值

试题解析：　解　(1)解法一：∵P是等腰直角三角形PBC的直角顶点，且BC＝2，

∴∠PCB＝，PC＝，

又∵∠ACB＝，∴∠ACP＝，

在△PAC中，由余弦定理得PA2＝AC2＋PC2－2AC·PCcos＝5，∴PA＝.

解法二：依题意建立如图直角坐标系，则有C(0,0)，B(2,0)，A(0,3)，

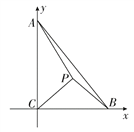∵△PBC是等腰直角三角形，∠ACB＝，

∴∠ACP＝，∠PBC＝，

∴直线PC的方程为y＝x，直线PB的方程为y＝－x＋2，

由得P(1,1)，

∴PA＝＝，

(2)在△PBC中，∠BPC＝，∠PCB＝θ，

∴∠PBC＝－θ，

由正弦定理得＝＝，

∴PB＝sinθ，PC＝sin，

∴△PBC的面积S(θ)＝PB·PCsin

＝sinsinθ

＝2sinθcosθ－sin2θ＝sin2θ＋cos2θ－

＝sin－，θ∈，

∴当θ＝时，△PBC面积的最大值为.