题目内容
在菱形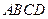 中,
中,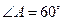 ,线段
,线段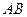 的中点是
的中点是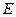 ,现将
,现将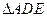 沿
沿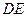 折起到
折起到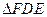 的位置,使平面
的位置,使平面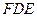 和平面
和平面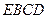 垂直,线段
垂直,线段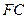 的中点是
的中点是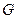 .
.
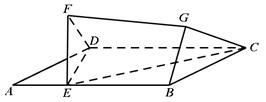
⑴证明:直线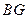 ∥平面
∥平面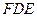 ;
;
⑵判断平面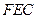 和平面
和平面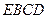 是否垂直,并证明你的结论.
是否垂直,并证明你的结论.
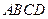 中,
中,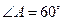 ,线段
,线段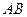 的中点是
的中点是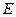 ,现将
,现将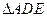 沿
沿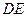 折起到
折起到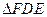 的位置,使平面
的位置,使平面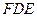 和平面
和平面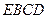 垂直,线段
垂直,线段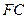 的中点是
的中点是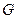 .
.
⑴证明:直线
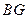 ∥平面
∥平面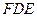 ;
;⑵判断平面
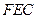 和平面
和平面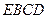 是否垂直,并证明你的结论.
是否垂直,并证明你的结论.(1)证明略
(2)垂直
略

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
题目内容
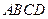 中,
中,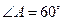 ,线段
,线段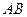 的中点是
的中点是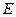 ,现将
,现将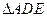 沿
沿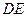 折起到
折起到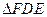 的位置,使平面
的位置,使平面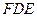 和平面
和平面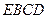 垂直,线段
垂直,线段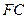 的中点是
的中点是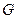 .
.
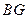 ∥平面
∥平面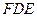 ;
;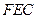 和平面
和平面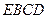 是否垂直,并证明你的结论.
是否垂直,并证明你的结论.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案