题目内容
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,
AN⊥PC于N.
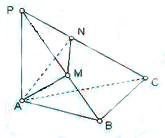
(1)求证:BC⊥面PAC;
(2)求证:PB⊥面AMN.
(3)若PA=AB=4,设∠BPC=θ,试用tanθ表示△AMN的面积,当tanθ取何值时,△AMN的面积最大?最大面积是多少?
AN⊥PC于N.

(1)求证:BC⊥面PAC;
(2)求证:PB⊥面AMN.
(3)若PA=AB=4,设∠BPC=θ,试用tanθ表示△AMN的面积,当tanθ取何值时,△AMN的面积最大?最大面积是多少?
(1)证明:∵PA⊥平面ABC,BC 平面ABC.
平面ABC.
∴PA⊥BC,又AB为斜边,∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC.
(2)证明:∵BC⊥平面PAC,AN 平面PAC ∴BC⊥AN,又AN⊥PC,且BC∩PC=C,
平面PAC ∴BC⊥AN,又AN⊥PC,且BC∩PC=C,
∴AN⊥面PBC,又PB 平面PBC.∴AN⊥PB,
平面PBC.∴AN⊥PB,
又∵PB⊥AM,AM∩AN=A,∴PB⊥平面AMN.
(3)解:在Rt△PAB中,PA=AB=4,∴PB=4 ,
,
∵PM⊥AB,∴AM= PB=2
PB=2 ,∴PM=BM=2
,∴PM=BM=2
又∵PB⊥面AMN,MN 平面AMN.∴PB⊥MN,
平面AMN.∴PB⊥MN,
∵MN=PM·tanθ=2 tanθ,∵AN⊥平面PBC,MN
tanθ,∵AN⊥平面PBC,MN 平面PBC.∴AN⊥MN
平面PBC.∴AN⊥MN
∵AN=

∴当tan2θ= ,即tanθ=
,即tanθ= 时,S△AMN有最大值为2,
时,S△AMN有最大值为2,
∴当tanθ= 时,S△AMN面积最大,最大值为2.
时,S△AMN面积最大,最大值为2.
 平面ABC.
平面ABC.∴PA⊥BC,又AB为斜边,∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC.
(2)证明:∵BC⊥平面PAC,AN
 平面PAC ∴BC⊥AN,又AN⊥PC,且BC∩PC=C,
平面PAC ∴BC⊥AN,又AN⊥PC,且BC∩PC=C,∴AN⊥面PBC,又PB
 平面PBC.∴AN⊥PB,
平面PBC.∴AN⊥PB,又∵PB⊥AM,AM∩AN=A,∴PB⊥平面AMN.
(3)解:在Rt△PAB中,PA=AB=4,∴PB=4
 ,
,∵PM⊥AB,∴AM=
 PB=2
PB=2 ,∴PM=BM=2
,∴PM=BM=2
又∵PB⊥面AMN,MN
 平面AMN.∴PB⊥MN,
平面AMN.∴PB⊥MN,∵MN=PM·tanθ=2
 tanθ,∵AN⊥平面PBC,MN
tanθ,∵AN⊥平面PBC,MN 平面PBC.∴AN⊥MN
平面PBC.∴AN⊥MN∵AN=


∴当tan2θ=
 ,即tanθ=
,即tanθ= 时,S△AMN有最大值为2,
时,S△AMN有最大值为2,∴当tanθ=
 时,S△AMN面积最大,最大值为2.
时,S△AMN面积最大,最大值为2.略

练习册系列答案
相关题目
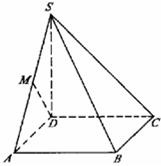
 的底面
的底面 是正方形,侧面
是正方形,侧面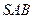 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面,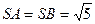 ,
, ,
,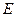 、
、 分别是
分别是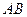 、
、 的中点。
的中点。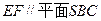 ;
;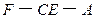 的大小。
的大小。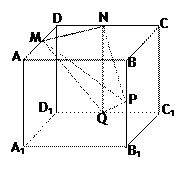
 锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB
锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB ,PC的中点.
,PC的中点. (3)在(2)的条件下,若AB=2,AC=
(3)在(2)的条件下,若AB=2,AC= ,求三棱锥P-ABC的体积
,求三棱锥P-ABC的体积
 .
.

 的中点。
的中点。 (1)求直线
(1)求直线
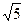 的等腰三角形,则二面角V―AB―C的度数是 。
的等腰三角形,则二面角V―AB―C的度数是 。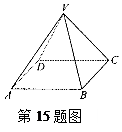
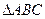 的中线
的中线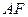 与中位线
与中位线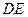 相交
相交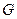 ,
,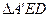 是
是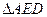 绕
绕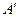 不与
不与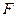 重合).现给出下列四个命题:
重合).现给出下列四个命题: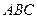 上的射影在线段
上的射影在线段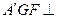 平面
平面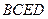 ;
; 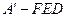 的体积有最大值;
的体积有最大值;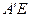 与
与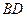 不可能垂直.其中正确的命题的序号是_________.
不可能垂直.其中正确的命题的序号是_________.