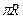题目内容
(本小题满分12分)
如图:已知△PAB所在的平面与菱形ABCD所在的平面垂直,且PA=PB=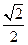 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点.
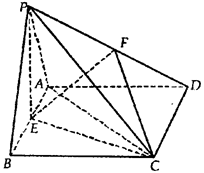
(Ⅰ)证明:CE⊥PA;
(Ⅱ)若F为线段PD上的点,且EF与平面PEC的
夹角为45°,求平面EFC与平面PBC夹角的
余弦值.
如图:已知△PAB所在的平面与菱形ABCD所在的平面垂直,且PA=PB=
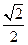 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点. 
(Ⅰ)证明:CE⊥PA;
(Ⅱ)若F为线段PD上的点,且EF与平面PEC的
夹角为45°,求平面EFC与平面PBC夹角的
余弦值.
解:(Ⅰ)在菱形ABCD中,∵
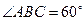
∴△ABC为正三角形,
又∵E为AB的中点
∴
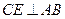 ,
,∵平面PAB^平面ABCD,AB为平面PAB与平面ABCD的交线,
∴
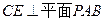 ,又∵
,又∵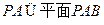
∴
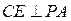 ┈┈┈┈┈4分
┈┈┈┈┈4分(Ⅱ)∵
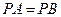 ,E为AB的中点,
,E为AB的中点,∴
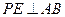 ,又∵
,又∵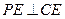 ,
,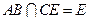
∴
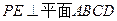 ,
,以E为坐标原点,
 所在直线分别为
所在直线分别为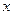 轴,
轴,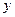 轴,
轴,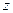 轴
轴建立空间直角坐标系如图所示

设
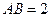 ,则
,则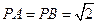 ,
,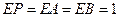 ,
,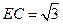 ,
,∴
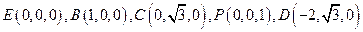
设
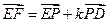 ,其中
,其中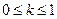 ,则
,则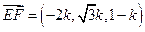 ,∵
,∵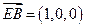 为平面
为平面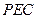 的法向量,∴
的法向量,∴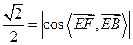 ,得
,得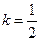 ,
,即
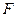 是
是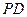 的中点,∴
的中点,∴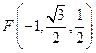 ┈┈┈┈┈9分
┈┈┈┈┈9分设
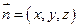 为平面
为平面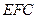 的法向量,则
的法向量,则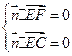
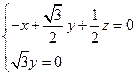 令
令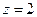 ,得
,得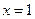 ,取
,取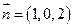 ,
,设
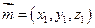 为平面
为平面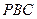 的法向量,则
的法向量,则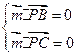 得出
得出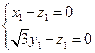
令
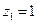 ,得
,得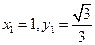 ,取
,取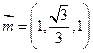 ,
,设平面
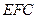 与平面
与平面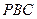 夹角为
夹角为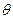 ,则
,则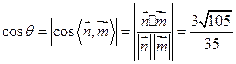 ┈┈┈12分
┈┈┈12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 沿BD将
沿BD将 折起,使面
折起,使面 面
面 ,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对
,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对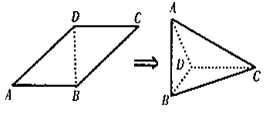

 的底面
的底面 是正方形,侧面
是正方形,侧面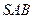 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面,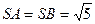 ,
, ,
, 、
、 分别是
分别是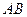 、
、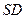 的中点。
的中点。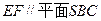 ;
;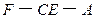 的大小。
的大小。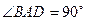 ,AD//BC, AB=
,AD//BC, AB= BC=1,AD=2,PA
BC=1,AD=2,PA 底面ABCD,PD与底面成
底面ABCD,PD与底面成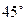 角,点E是PD的中点.
角,点E是PD的中点.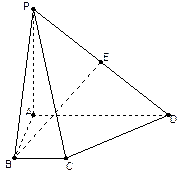
 中,
中,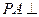 底面ABC,
底面ABC,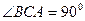 ,
,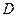 ,
, 分别在棱
分别在棱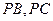 上,且BC//平面ADE
上,且BC//平面ADE 证:DE⊥平面
证:DE⊥平面
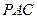 ;
;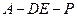 为直二面角时,求多面体ABCED与PAED的体积比。
为直二面角时,求多面体ABCED与PAED的体积比。 锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB
锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB ,PC的中点.
,PC的中点. (3)在(2)的条件下,若AB=2,AC=
(3)在(2)的条件下,若AB=2,AC= ,求三棱锥P-ABC的体积
,求三棱锥P-ABC的体积
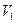 和
和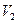 ,则
,则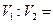 ( )
( ) 纬
纬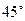 圈上有甲、乙两地,甲地位于东经
圈上有甲、乙两地,甲地位于东经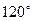 ,乙地位于西经
,乙地位于西经 , 则地球(半径为R)表面上甲、乙两地的最短距离是
, 则地球(半径为R)表面上甲、乙两地的最短距离是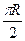 B.
B. 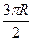 C.
C. 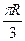 D.
D.