题目内容
已知点O为正方体ABCD—A1B1C1D1底面ABCD的中心,则下列结论正确的是( )
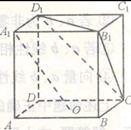

A.直线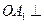 平面AB1C1 平面AB1C1 | B.直线OA1//直线BD1 |
C.直线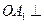 直线AD 直线AD | D.直线OA1//平面CB1D1 |
D
略

练习册系列答案
相关题目
题目内容

A.直线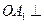 平面AB1C1 平面AB1C1 | B.直线OA1//直线BD1 |
C.直线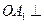 直线AD 直线AD | D.直线OA1//平面CB1D1 |
