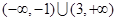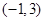题目内容
设不等式组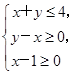 表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )
表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )
A.[2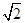 ,2
,2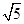 ] B.[2
] B.[2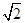 ,3
,3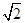 ] C.[3
] C.[3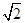 ,2
,2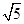 ] D.(0,2
] D.(0,2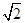 )∪(2
)∪(2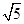 ,+∞)
,+∞)
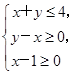 表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )
表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )A.[2
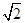 ,2
,2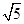 ] B.[2
] B.[2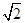 ,3
,3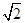 ] C.[3
] C.[3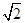 ,2
,2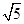 ] D.(0,2
] D.(0,2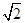 )∪(2
)∪(2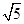 ,+∞)
,+∞)D
不等式组对应的区域D为△ABE,

圆C的圆心为(-1,-1).区域D中,A到圆心的距离最小,B到圆心的距离最大,所以要使圆不经过区域D,则有0<r<|AC|或r>|BC|.
由 得
得 即A(1,1),由
即A(1,1),由 得
得
即B(1,3),所以|AC|=2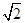 ,|BC|=2
,|BC|=2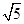 ,所以0<r<2
,所以0<r<2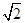 或r>2
或r>2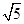 ,即r的取值范围是(0,2
,即r的取值范围是(0,2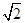 )∪(2
)∪(2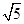 ,+∞).
,+∞).

圆C的圆心为(-1,-1).区域D中,A到圆心的距离最小,B到圆心的距离最大,所以要使圆不经过区域D,则有0<r<|AC|或r>|BC|.
由
 得
得 即A(1,1),由
即A(1,1),由 得
得
即B(1,3),所以|AC|=2
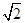 ,|BC|=2
,|BC|=2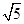 ,所以0<r<2
,所以0<r<2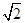 或r>2
或r>2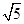 ,即r的取值范围是(0,2
,即r的取值范围是(0,2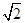 )∪(2
)∪(2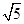 ,+∞).
,+∞).
练习册系列答案
相关题目
 所表示的平面区域为
所表示的平面区域为 ,记
,记 . 则
. 则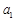 = ,经推理可得到
= ,经推理可得到 = .
= . ,则目标函数
,则目标函数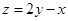 的最小值为 。
的最小值为 。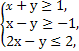 且目标函数z=ax+by(a>0,b>0)的最大值为7,则
且目标函数z=ax+by(a>0,b>0)的最大值为7,则 +
+ 的最小值为( )
的最小值为( ) >2;
>2;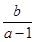 的取值范围为
的取值范围为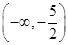 ∪
∪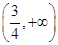 .
.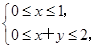 则点Q(x+y,y)构成的图形的面积为( )
则点Q(x+y,y)构成的图形的面积为( ) ,若目标函数
,若目标函数 (
( )的最大值为8,则
)的最大值为8,则 的最小值为 .
的最小值为 .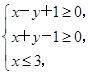 则z=2x-3y的最小值是( ).
则z=2x-3y的最小值是( ). 表示的平面区域是以直线
表示的平面区域是以直线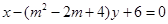 为界的两个平面区域中的一个,且点
为界的两个平面区域中的一个,且点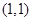 在这个区域内,则实数
在这个区域内,则实数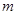 的取值范围是( )
的取值范围是( )