题目内容
若x,y满足约束条件 且目标函数z=ax+by(a>0,b>0)的最大值为7,则
且目标函数z=ax+by(a>0,b>0)的最大值为7,则 +
+ 的最小值为( )
的最小值为( )
 且目标函数z=ax+by(a>0,b>0)的最大值为7,则
且目标函数z=ax+by(a>0,b>0)的最大值为7,则 +
+ 的最小值为( )
的最小值为( )| A.14 | B.7 | C.18 | D.13 |
B
画出可行域,对目标函数分析得到最优解,从而根据已知条件代入得到a,b满足的条件,然后利用“1的代换”方法,使用基本不等式求得最小值.
画出可行域如图所示,

由图形可知当直线经过x-y=-1与2x-y=2的交点N(3,4)时,目标函数取得最大值,即3a+4b=7,于是 +
+ =
= (3a+4b)(
(3a+4b)( +
+ )=
)= (25+
(25+ +
+ )≥
)≥ (25+2
(25+2 )=7,即
)=7,即 +
+ 的最小值为7.
的最小值为7.
画出可行域如图所示,

由图形可知当直线经过x-y=-1与2x-y=2的交点N(3,4)时,目标函数取得最大值,即3a+4b=7,于是
 +
+ =
= (3a+4b)(
(3a+4b)( +
+ )=
)= (25+
(25+ +
+ )≥
)≥ (25+2
(25+2 )=7,即
)=7,即 +
+ 的最小值为7.
的最小值为7.
练习册系列答案
相关题目
 满足约束条件
满足约束条件 则
则 的取值范围是.
的取值范围是.
 ,试求解下列问题.
,试求解下列问题. 的最大值和最小值;
的最大值和最小值; 的最大值和最小值;
的最大值和最小值; 所表示的平面区域的面积是________.
所表示的平面区域的面积是________.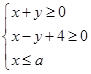 所表示的平面区域的面积是9,则实数a的值为____.
所表示的平面区域的面积是9,则实数a的值为____.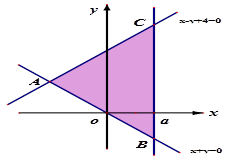
 则目标函数z=3x-y的取值范围是( )
则目标函数z=3x-y的取值范围是( ) ,6]
,6]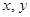 满足
满足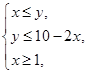 向量
向量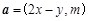 ,
,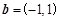 .若
.若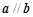 ,则实数
,则实数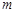 的最大值为 .
的最大值为 .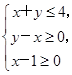 表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )
表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )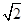 ,2
,2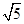 ] B.[2
] B.[2 所表示的平面区域是面积为1的直角三角形,则z=x-2y的最大值是( ).
所表示的平面区域是面积为1的直角三角形,则z=x-2y的最大值是( ).