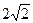题目内容
已知直线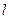 过坐标原点,抛物线
过坐标原点,抛物线 的顶点在原点,焦点在
的顶点在原点,焦点在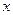 轴正半轴上,若点
轴正半轴上,若点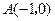 和点
和点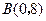 关于
关于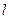 的对称点都在
的对称点都在 上,求直线
上,求直线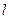 和抛物线
和抛物线 的方程.
的方程.
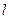 过坐标原点,抛物线
过坐标原点,抛物线 的顶点在原点,焦点在
的顶点在原点,焦点在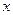 轴正半轴上,若点
轴正半轴上,若点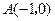 和点
和点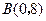 关于
关于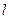 的对称点都在
的对称点都在 上,求直线
上,求直线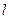 和抛物线
和抛物线 的方程.
的方程.直线方程为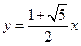 ,抛物线方程为
,抛物线方程为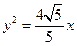
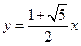 ,抛物线方程为
,抛物线方程为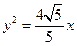
依题意设抛物线 的方程可写为
的方程可写为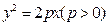 ,且
,且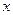 轴和
轴和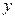 轴不是所求直线.
轴不是所求直线.
又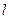 过原点,因而可设
过原点,因而可设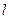 的方程为
的方程为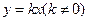 ①
①
设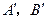 分别是
分别是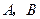 关于
关于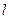 的对称点,因而
的对称点,因而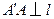 ,
,
直线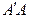 的方程为
的方程为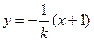 ②
②
由①,②联立解得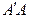 与
与 的交点
的交点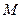 的坐标为
的坐标为 .
.
又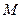 为
为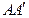 的中点,从而点
的中点,从而点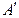 的坐标为
的坐标为
 ③
③
同理得点 的坐标为
的坐标为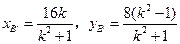 ④
④
又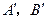 均为抛物线
均为抛物线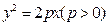 上,由③得
上,由③得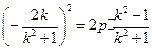 ,
,
由此知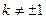 ,即
,即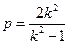 ⑤
⑤
同理由④得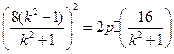 ,即
,即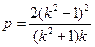 ,
,
从而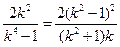 ,整理得
,整理得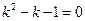 .
.
解得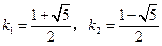 .
.
但当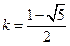 时,由③知
时,由③知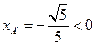 .
.
这与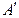 在抛物线
在抛物线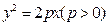 上矛盾,故舍去
上矛盾,故舍去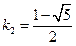 .
.
设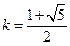 ,则直线
,则直线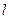 的方程为
的方程为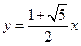 .
.
将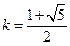 代入⑤,求得
代入⑤,求得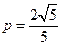 .
.
所以直线方程为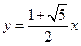 ,抛物线方程为
,抛物线方程为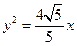 .
.
 的方程可写为
的方程可写为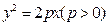 ,且
,且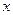 轴和
轴和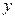 轴不是所求直线.
轴不是所求直线.又
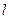 过原点,因而可设
过原点,因而可设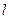 的方程为
的方程为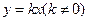 ①
①设
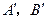 分别是
分别是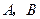 关于
关于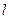 的对称点,因而
的对称点,因而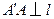 ,
,直线
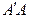 的方程为
的方程为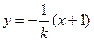 ②
②由①,②联立解得
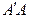 与
与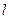 的交点
的交点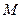 的坐标为
的坐标为 .
.又
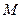 为
为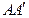 的中点,从而点
的中点,从而点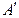 的坐标为
的坐标为 ③
③同理得点
 的坐标为
的坐标为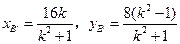 ④
④又
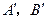 均为抛物线
均为抛物线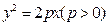 上,由③得
上,由③得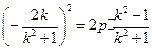 ,
,由此知
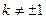 ,即
,即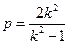 ⑤
⑤同理由④得
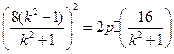 ,即
,即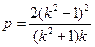 ,
,从而
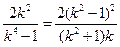 ,整理得
,整理得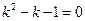 .
.解得
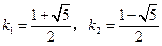 .
.但当
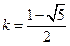 时,由③知
时,由③知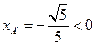 .
.这与
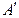 在抛物线
在抛物线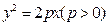 上矛盾,故舍去
上矛盾,故舍去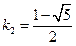 .
.设
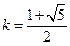 ,则直线
,则直线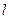 的方程为
的方程为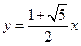 .
.将
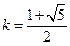 代入⑤,求得
代入⑤,求得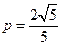 .
.所以直线方程为
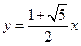 ,抛物线方程为
,抛物线方程为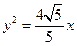 .
.
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
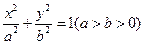 的左、右焦点分别是
的左、右焦点分别是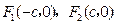 ,
,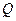 是椭圆外的动点,满足
是椭圆外的动点,满足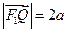 ,点
,点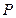 是线段
是线段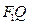 与该椭圆的交点,设
与该椭圆的交点,设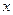 为点
为点 。
。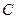 的中心在坐标原点,左顶点
的中心在坐标原点,左顶点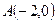 ,离心率
,离心率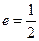 ,
,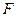 为右焦点,过焦点
为右焦点,过焦点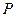 、
、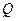 两点(不同于点
两点(不同于点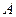 ).
).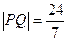 时,求直线PQ的方程;
时,求直线PQ的方程;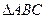 能否成为等边三角形,并说明理由.
能否成为等边三角形,并说明理由.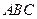 的顶点
的顶点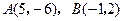 ,求
,求 的外接圆方程.
的外接圆方程.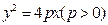 的准线与
的准线与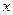 轴的交点为
轴的交点为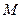 ,过点
,过点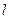 交抛物线于
交抛物线于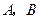 两点.
两点.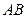 中点的轨迹方程;
中点的轨迹方程;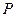 到两个定点
到两个定点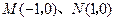 距离的比为
距离的比为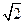 ,点
,点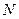 到直线
到直线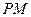 的距离为1.求直线
的距离为1.求直线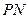 的方程.
的方程. 和双曲线
和双曲线 有公共的焦点,(1)求双曲线的渐近线方程(2)直线
有公共的焦点,(1)求双曲线的渐近线方程(2)直线 过焦点且垂直于x轴,若直线
过焦点且垂直于x轴,若直线 ,求双曲线的方程
,求双曲线的方程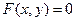 的点都在曲线
的点都在曲线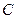 上,那么 ( )
上,那么 ( )