题目内容
(本小题满分12分)已知函数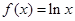 ,
,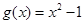 ,
,
(1)求函数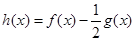 的最值;
的最值;
(2)对于一切正数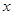 ,恒有
,恒有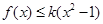 成立,求实数
成立,求实数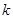 的取值组成的集合。
的取值组成的集合。
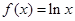 ,
,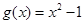 ,
,(1)求函数
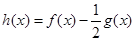 的最值;
的最值;(2)对于一切正数
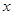 ,恒有
,恒有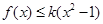 成立,求实数
成立,求实数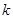 的取值组成的集合。
的取值组成的集合。(1)函数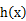 在(0,1)递增,在
在(0,1)递增,在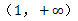 递减。
递减。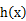 的最大值为
的最大值为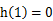 .
.
(2)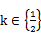 。
。
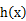 在(0,1)递增,在
在(0,1)递增,在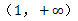 递减。
递减。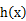 的最大值为
的最大值为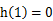 .
. (2)
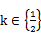 。
。本试题主要是考查了导数在研究函数中的运用。
(1)求解导数,然后根据导数的符号与函数单调性的关系得到判定,求解极值和最值。
(2)要证明不等式恒成立,那么可以通过研究函数的最值来分析得到参数的范围。
解:(1)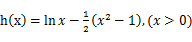
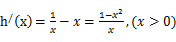
所以可知函数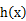 在(0,1)递增,在
在(0,1)递增,在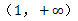 递减。
递减。
所以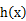 的最大值为
的最大值为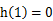 .
.
(2)令函数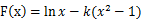
得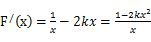
当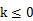 时,
时,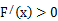 恒成立。所以
恒成立。所以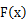 在
在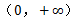 递增,
递增,
故x>1时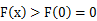 不满足题意。
不满足题意。
当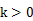 时,当
时,当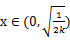 时
时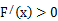 恒成立,函数
恒成立,函数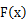 递增;
递增;
当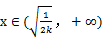 时
时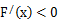 恒成立,函数
恒成立,函数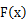 递减。
递减。
所以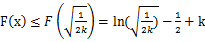 ;即
;即 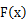 的最大值
的最大值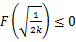
令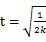 ,则
,则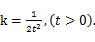
令函数 ,
, 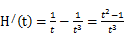
所以当 时,函数
时,函数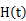 递减;当
递减;当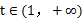 时,函数
时,函数 递增;
递增;
所以函数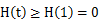 ,
,
从而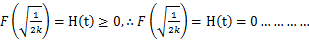
就必须当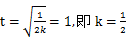 时成立。
时成立。
综上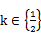 。
。
(1)求解导数,然后根据导数的符号与函数单调性的关系得到判定,求解极值和最值。
(2)要证明不等式恒成立,那么可以通过研究函数的最值来分析得到参数的范围。
解:(1)
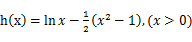
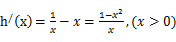
所以可知函数
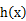 在(0,1)递增,在
在(0,1)递增,在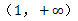 递减。
递减。所以
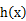 的最大值为
的最大值为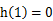 .
. (2)令函数
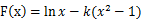
得
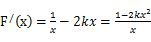
当
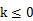 时,
时,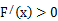 恒成立。所以
恒成立。所以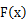 在
在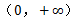 递增,
递增,故x>1时
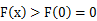 不满足题意。
不满足题意。当
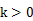 时,当
时,当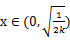 时
时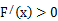 恒成立,函数
恒成立,函数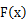 递增;
递增;当
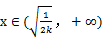 时
时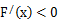 恒成立,函数
恒成立,函数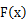 递减。
递减。所以
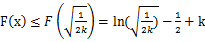 ;即
;即 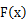 的最大值
的最大值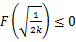
令
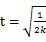 ,则
,则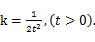
令函数
 ,
, 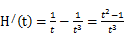
所以当
 时,函数
时,函数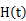 递减;当
递减;当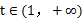 时,函数
时,函数 递增;
递增;所以函数
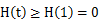 ,
,从而
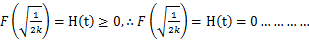
就必须当
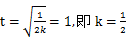 时成立。
时成立。综上
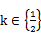 。
。
练习册系列答案
相关题目
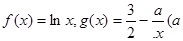 为实常数).
为实常数).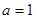 时,求函数
时,求函数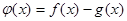 在
在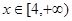 上的最小值;
上的最小值;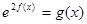 在区间
在区间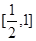 上有解,求实数
上有解,求实数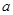 的取值范围;
的取值范围;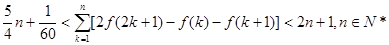
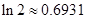 )
) 在点
在点 的切线方程为
的切线方程为 .
. 的解析式;
的解析式; ,求证:
,求证: 在
在 上恒成立.
上恒成立.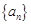 的首项
的首项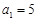 ,且
,且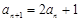 .
.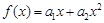 …
…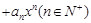 ,求
,求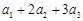 …
…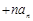 .
. 在
在 上是增函数,在
上是增函数,在 上是减函数.
上是减函数. 的解析式;
的解析式; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,使得方程
,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出
上恰有两个相异实数根,若存在,求出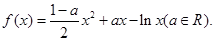 (Ⅰ) 当
(Ⅰ) 当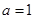 时,求函数
时,求函数 的极值;
的极值;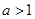 时,讨论函数
时,讨论函数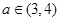 及任意
及任意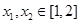 ,恒有
,恒有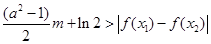 成立,求实数
成立,求实数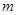 的取值范围.
的取值范围.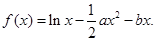
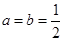 时,求函数
时,求函数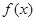 的最大值;
的最大值;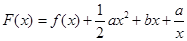 ,(
,(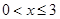 )其图象上任意一点
)其图象上任意一点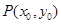 处切线的斜率
处切线的斜率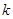 ≤
≤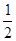 恒成立,求实数
恒成立,求实数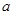 的取值范围;
的取值范围;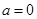 ,
,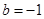 ,方程
,方程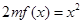 有唯一实数解,求正数
有唯一实数解,求正数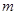 的值.
的值.  .(
.(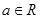 ).
).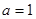 时,求函数
时,求函数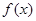 的极值;
的极值;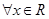 ,有
,有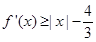 成立,求实数
成立,求实数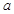 的取值范围.
的取值范围.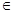 R为常数.
R为常数. 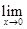
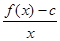 =4,试证:-6≤b≤2.
=4,试证:-6≤b≤2.