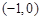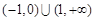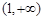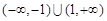题目内容
(本小题满分12分)
已知函数 .(
.(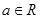 ).
).
(1)当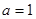 时,求函数
时,求函数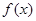 的极值;
的极值;
(2)若对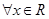 ,有
,有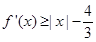 成立,求实数
成立,求实数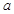 的取值范围.
的取值范围.
已知函数
 .(
.(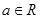 ).
).(1)当
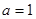 时,求函数
时,求函数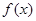 的极值;
的极值;(2)若对
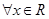 ,有
,有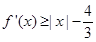 成立,求实数
成立,求实数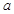 的取值范围.
的取值范围.(1)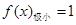 ,
,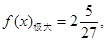 (2)
(2)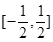
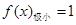 ,
,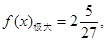 (2)
(2)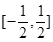
(1)当a=1时,可利用导数研究其极值,根据极值点左正右负为极大值,极值点左负右正为极小值,确定其极值.
(2)本小题实质是由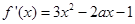 ,∴对
,∴对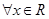 ,
,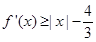 成立,
成立,
即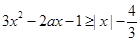 对
对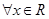 成立,然后再对x讨论去绝对值分离常数进一步转化为不等式恒成立问题来解决.
成立,然后再对x讨论去绝对值分离常数进一步转化为不等式恒成立问题来解决.
解:(1)当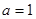 时,
时,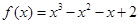
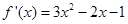 =
=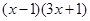 ,----------------------------2分
,----------------------------2分
令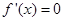 ,解得
,解得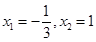 .
.
当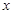 变化时,
变化时,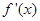 ,
,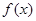 的变化情况如下表:
的变化情况如下表:
------------------------4分
∴当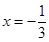 时,函数
时,函数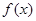 有极大值,
有极大值,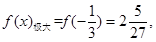 ----------------5分
----------------5分
当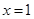 时函数
时函数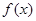 有极小值,
有极小值,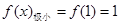 ---------------------------6分
---------------------------6分
(2)∵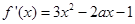 ,∴对
,∴对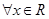 ,
,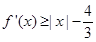 成立,
成立,
即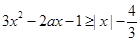 对
对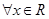 成立,----------------------------------7分
成立,----------------------------------7分
①当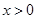 时,有
时,有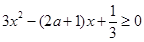 ,
,
即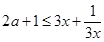 ,对
,对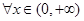 恒成立, -----------------8分
恒成立, -----------------8分
∵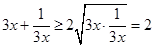 ,当且仅当
,当且仅当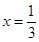 时等号成立,
时等号成立,
∴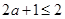
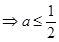 ---------------------9分
---------------------9分
②当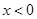 时,有
时,有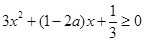 ,
,
即 ,对
,对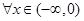 恒成立,
恒成立,
∵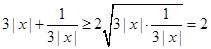 ,当且仅当
,当且仅当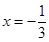 时等号成立,
时等号成立,
∴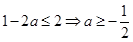 ----------11分
----------11分
③当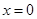 时,
时,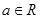
综上得实数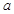 的取值范围为
的取值范围为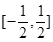 .----------------12分
.----------------12分
(2)本小题实质是由
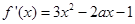 ,∴对
,∴对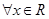 ,
,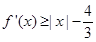 成立,
成立,即
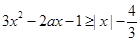 对
对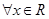 成立,然后再对x讨论去绝对值分离常数进一步转化为不等式恒成立问题来解决.
成立,然后再对x讨论去绝对值分离常数进一步转化为不等式恒成立问题来解决.解:(1)当
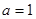 时,
时,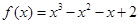
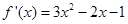 =
=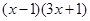 ,----------------------------2分
,----------------------------2分令
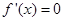 ,解得
,解得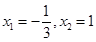 .
.当
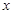 变化时,
变化时,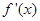 ,
,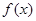 的变化情况如下表:
的变化情况如下表:| x | 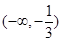 | 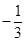 | 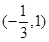 | 1 | 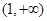 |
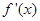 | + | 0 |  | 0 | + |
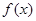 | 单调递增 | 极大 | 单调递减 | 极小 | 单调递增 |
∴当
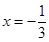 时,函数
时,函数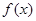 有极大值,
有极大值,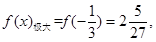 ----------------5分
----------------5分当
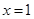 时函数
时函数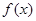 有极小值,
有极小值,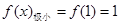 ---------------------------6分
---------------------------6分(2)∵
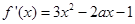 ,∴对
,∴对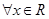 ,
,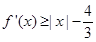 成立,
成立,即
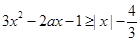 对
对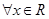 成立,----------------------------------7分
成立,----------------------------------7分①当
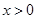 时,有
时,有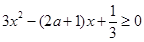 ,
,即
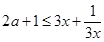 ,对
,对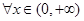 恒成立, -----------------8分
恒成立, -----------------8分∵
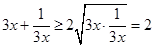 ,当且仅当
,当且仅当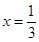 时等号成立,
时等号成立,∴
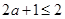
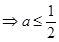 ---------------------9分
---------------------9分②当
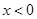 时,有
时,有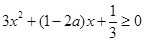 ,
,即
 ,对
,对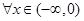 恒成立,
恒成立,∵
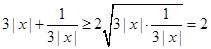 ,当且仅当
,当且仅当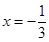 时等号成立,
时等号成立,∴
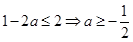 ----------11分
----------11分③当
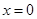 时,
时,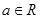
综上得实数
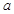 的取值范围为
的取值范围为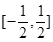 .----------------12分
.----------------12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与1的大小;
与1的大小;
 .
. (
(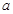 为实常数)。
为实常数)。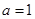 时,求函数
时,求函数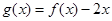 的单调区间;
的单调区间;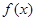 在区间
在区间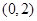 上无极值,求
上无极值,求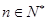 且
且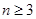 ,求证:
,求证: 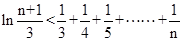 .
.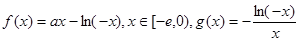 ,其中
,其中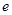 是自然对数的底数,
是自然对数的底数,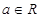
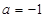 时,
时,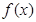 的单调性。
的单调性。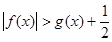
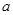 ,使
,使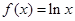 ,
,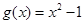 ,
,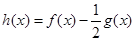 的最值;
的最值;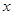 ,恒有
,恒有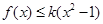 成立,求实数
成立,求实数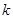 的取值组成的集合。
的取值组成的集合。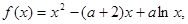
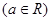
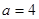 ,方程
,方程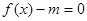 有三个不同的根,求
有三个不同的根,求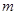 的取值范围。
的取值范围。 +6x的图象关于y轴对称.
+6x的图象关于y轴对称.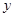 =
=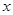 +
+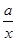 有如下性质:如果常数
有如下性质:如果常数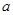 >0,那么该函数在
>0,那么该函数在 0,
0,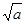
 上是减函数,在
上是减函数,在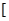
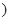 上是增函数.
上是增函数.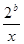 (
(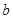 的值;
的值;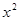 +
+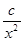 (常数
(常数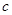 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;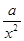 (常数
(常数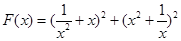 (
(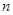 是正整数)在区间[
是正整数)在区间[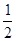 ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).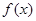 满足
满足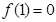 ,当
,当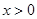 时有
时有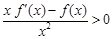 ,则不等式
,则不等式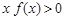 的解集为( )
的解集为( )