题目内容
【题目】已知函数 
，a为正常数．
（1）若f（x）=lnx+φ（x），且a= 
，求函数f（x）的单调增区间；
（2）在（1）中当a=0时，函数y=f（x）的图象上任意不同的两点A（x1 ， y1），B（x2 ， y2），线段AB的中点为C（x0 ， y0），记直线AB的斜率为k，试证明：k＞f'（x0）．
（3）若g（x）=|lnx|+φ（x），且对任意的x1 ， x2∈（0，2]，x1≠x2 ， 都有 
，求a的取值范围．
【答案】
（1）解： 
∵a= 
，令f'（x）＞0得x＞2或 
∴函数f（x）的单调增区间为 
（2）解：证明：当a=0时f（x）=lnx
∴ 
∴ 
又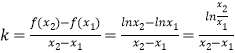 
不妨设x2＞x1，要比较k与f'（x0）的大小，
即比较 
与 
的大小，
又∵x2＞x1，
∴即比较 
与 
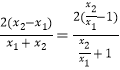的大小．
令 
，
则 
∴h（x）在[1，+∞）上是增函数．
又 
，
∴ 
，
∴ 
，
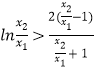即k＞f'（x0）；
（3）解：∵ 
，
∴ 
由题意得F（x）=g（x）+x在区间（0，2]上是减函数．
1°当 
，
∴ 
由 
在x∈[1，2]恒成立．
设m（x）= 
，x∈[1，2]，则 
∴m（x）在[1，2]上为增函数，
∴ 
2°当 
，
∴
由 
在x∈（0，1）恒成立
设t（x）= 
，x∈（0，1）为增函数
∴a≥t（1）=0
综上：a的取值范围为 
【解析】（1）由题意先把f（x）的解析式具体，然后求其导函数，令导函数大于0，解出的即为函数的增区间；（2）对于当a=0时，先把f（x）=lnx具体出来，然后求导函数，得到f′（x0），在利用斜率公式求出过这两点的斜率公式，利用构造函数并利用构造函数的单调性比较大小；（3）因为g（x）=|lnx|+φ（x），且对任意的x1 ， x2∈（0，2]，x1≠x2 ， 都有 ，先写出g（x）的解析式，利用该函数的单调性把问题转化为恒成立问题进行求解．
【考点精析】解答此题的关键在于理解函数的单调性的相关知识，掌握注意：函数的单调性是函数的局部性质；函数的单调性还有单调不增，和单调不减两种，以及对函数单调性的性质的理解，了解函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集．
