题目内容
【题目】已知函数f(x)=4cosωx·sin(ωx+![]() )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间[0,![]() ]上的单调性.
]上的单调性.
【答案】(1)ω=1
(2)f(x)在区间[0,![]() ]上单调递增,在区间[
]上单调递增,在区间[![]() ,
,![]() ]上单调递减.
]上单调递减.
【解析】解:(1)f(x)=4cosωx·sin(ωx+![]() )
)
=2![]() sinωx·cosωx+2
sinωx·cosωx+2![]() cos2ωx
cos2ωx
=![]() (sin2ωx+cos2ωx)+
(sin2ωx+cos2ωx)+![]()
=2sin(2ωx+![]() )+
)+![]() .
.
∵f(x)的最小正周期为π,且ω>0,
从而有![]() =π,故ω=1.
=π,故ω=1.
(2)由(1)知f(x)=2sin(2x+![]() )+
)+![]() .
.
若0≤x≤![]() ,则
,则![]() ≤2x+
≤2x+![]() ≤
≤![]() .
.
当![]() ≤2x+
≤2x+![]() ≤
≤![]() ,即0≤x≤
,即0≤x≤![]() 时,f(x)单调递增;
时,f(x)单调递增;
当![]() ≤2x+
≤2x+![]() ≤
≤![]() ,即
,即![]() ≤x≤
≤x≤![]() 时,f(x)单调递减.
时,f(x)单调递减.
综上可知,f(x)在区间[0,![]() ]上单调递增,在区间[
]上单调递增,在区间[![]() ,
,![]() ]上单调递减.
]上单调递减.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
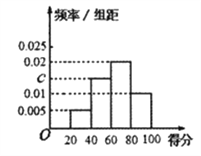
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校安全教育活动的成效.若
的方差)来评估该校安全教育活动的成效.若![]() ,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?