题目内容
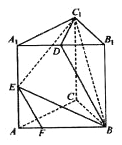
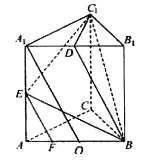
【题目】在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,且D,E分别是棱A1B1,AA1的中点,点F在棱AB上,且AF=![]() AB。
AB。
(1)求证:EF∥平面BDC1;
(2)求三棱锥D-BEC1的体积。
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)由题意结合几何关系可证得EF∥BD,然后利用线面平行的判定定理即可证得EF∥平面DBC1;
(2)利用题中几何体的特点转化顶点可求得三棱锥的体积为![]() .
.
试题解析:
(1)设O为AB的中点,连接A1O,∵AF= ![]() ,O为AB的中点,∴F为AO的中点,
,O为AB的中点,∴F为AO的中点,
又∵E为AA1的中点,∴EF∥A1O,又∵D为A1B1的中点,O为AB的中点,∴A1D=OB,
又∵A1D∥OB,所以四面形A1DBO为平行四边形,∴A1O∥BD,又∵EF∥A1O,∴EF∥BD,又∵EF![]() 平面DBC1,BD
平面DBC1,BD![]() 平面DBC1,∴EF∥平面DBC1;
平面DBC1,∴EF∥平面DBC1;
∵AB=BC-CA=AA1=2
D,E分别为A1B1,AA1的中点,AF=![]() AB,∴C1D⊥面ABB1A1,而
AB,∴C1D⊥面ABB1A1,而![]()
S△BDE=![]() =2x2-
=2x2-![]() x2x1-
x2x1-![]() x2x1-
x2x1-![]() x1x1=
x1x1=![]() 。
。
 ∵C1D=
∵C1D=![]() ,∴
,∴![]() =
=![]() S△BDE·C1D=
S△BDE·C1D=![]()

【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
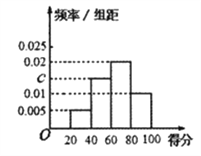
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校安全教育活动的成效.若
的方差)来评估该校安全教育活动的成效.若![]() ,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?