题目内容
【题目】综合题。
（1）已知复数z在复平面内对应的点在第四象限，|z|=1，且z+ 
=1，求z；
（2）已知复数z= 
﹣（1+5i）m﹣3（2+i）为纯虚数，求实数m的值．
【答案】
（1）解：设z=a+bi，a，b∈R，则由题意可得 
，解得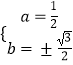 
．
再根据复数z在复平面内对应的点在第四象限，可得b=﹣ 
，∴z= 
﹣ i
（2）解：∵复数z= 
﹣（1+5i）m﹣3（2+i）=（m2﹣m﹣6）+（2m2﹣5m﹣3）i为纯虚数，
∴m2﹣m﹣6=0，且2m2﹣5m﹣3≠0，求得m=﹣2
【解析】（1）设z=a+bi，a，b∈R，则由题意可得 ，结合复数z在复平面内对应的点在第四象限，解得a、b的值．（2）化简复数z为（m2﹣m﹣6）+（2m2﹣5m﹣3）i，是纯虚数，可得m2﹣m﹣6=0，且2m2﹣5m﹣3≠0，由此求得m的值．
练习册系列答案
相关题目
